有人在Stack Exchange问了一个问题:
"我一直觉得虚数(imaginary number)很难懂。
中学老师说,虚数就是-1的平方根。
可是,什么数的平方等于-1呢?计算器直接显示出错!
直到今天,我也没有搞懂。谁能解释,虚数到底是什么?
它有什么用?"
帖子的下面,很多人给出了自己的解释,还推荐了一篇非常棒的文章《虚数的图解》。我读后恍然大悟,醍醐灌顶,原来虚数这么简单,一点也不奇怪和难懂!
下面,我就用自己的语言,讲述我所理解的虚数。
一、什么是虚数?
首先,假设有一根数轴,上面有两个反向的点:+1和-1。

这根数轴的正向部分,可以绕原点旋转。显然,逆时针旋转180度,+1就会变成-1。
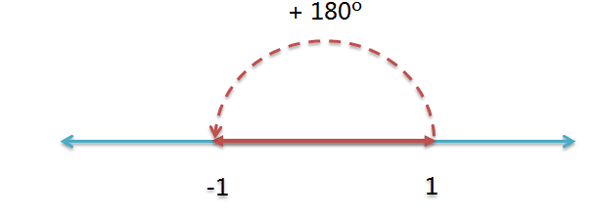
这相当于两次逆时针旋转90度。
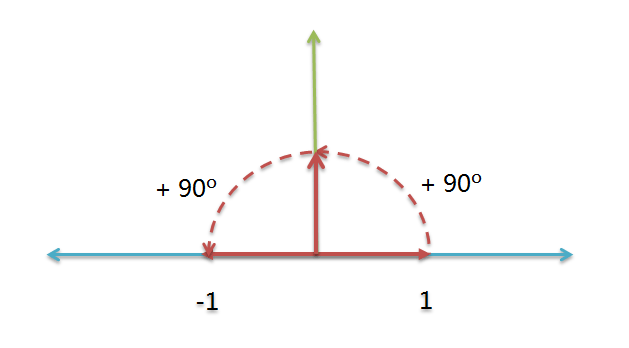
因此,我们可以得到下面的关系式:
(+1) * (逆时针旋转90度) * (逆时针旋转90度) = (-1)
如果把+1消去,这个式子就变为:
(逆时针旋转90度)^2 = (-1)
将"逆时针旋转90度"记为 i :
i^2 = (-1)
这个式子很眼熟,它就是虚数的定义公式。
所以,我们可以知道,虚数 i 就是逆时针旋转90度,i 不是一个数,而是一个旋转量。
二、复数的定义
既然 i 表示旋转量,我们就可以用 i ,表示任何实数的旋转状态。
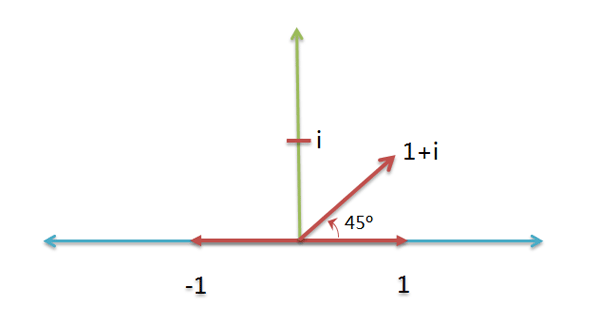
将实数轴看作横轴,虚数轴看作纵轴,就构成了一个二维平面。旋转到某一个角度的任何正实数,必然唯一对应这个平面中的某个点。
只要确定横坐标和纵坐标,比如( 1 , i ),就可以确定某个实数的旋转量(45度)。
数学家用一种特殊的表示方法,表示这个二维坐标:用 + 号把横坐标和纵坐标连接起来。比如,把 ( 1 , i ) 表示成 1 + i 。这种表示方法就叫做复数(complex number),其中 1 称为实数部,i 称为虚数部。
为什么要把二维坐标表示成这样呢,下一节告诉你原因。
三、虚数的作用:加法
虚数的引入,大大方便了涉及到旋转的计算。
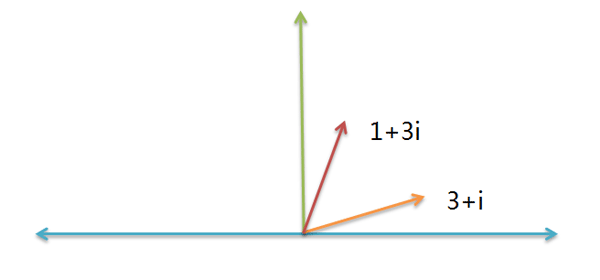
比如,物理学需要计算"力的合成"。假定一个力是 3 + i ,另一个力是 1 + 3i ,请问它们的合成力是多少?
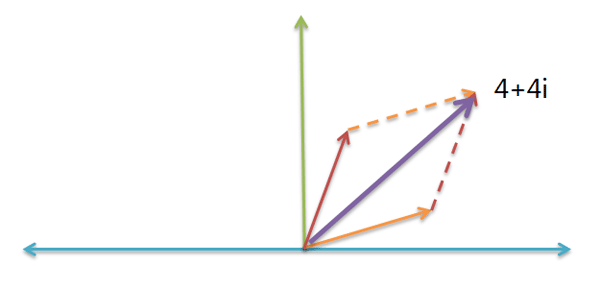
根据"平行四边形法则",你马上得到,合成力就是 ( 3 + i ) + ( 1 + 3i ) = ( 4 + 4i )。
这就是虚数加法的物理意义。
四、虚数的作用:乘法
如果涉及到旋转角度的改变,处理起来更方便。
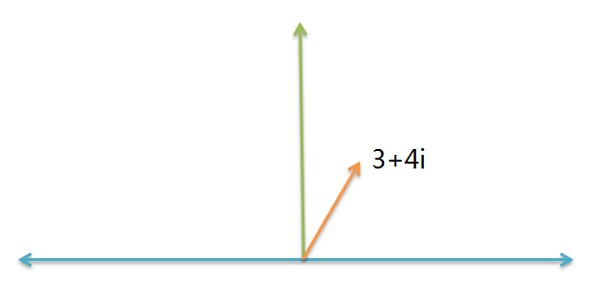
比如,一条船的航向是 3 + 4i 。
如果该船的航向,逆时针增加45度,请问新航向是多少?
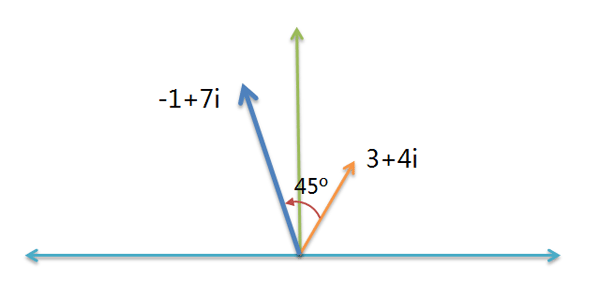
45度的航向就是 1 + i 。计算新航向,只要把这两个航向 3 + 4i 与 1 + i 相乘就可以了(原因在下一节解释):
( 3 + 4i ) * ( 1 + i ) = ( -1 + 7i )
所以,该船的新航向是 -1 + 7i 。
如果航向逆时针增加90度,就更简单了。因为90度的航向就是 i ,所以新航向等于:
( 3 + 4i ) * i = ( -4 + 3i )
这就是虚数乘法的物理意义:改变旋转角度。
五、虚数乘法的数学证明
为什么一个复数改变旋转角度,只要做乘法就可以了?
下面就是它的数学证明,实际上很简单。
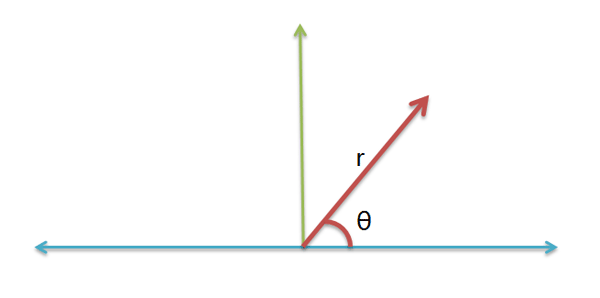
任何复数 a + bi,都可以改写成旋转半径 r 与横轴夹角 θ 的形式。
假定现有两个复数 a + bi 和 c + di,可以将它们改写如下:
a + bi = r1 * ( cosα + isinα )
c + di = r2 * ( cosβ + isinβ )
这两个复数相乘,( a + bi )( c + di ) 就相当于
r1 * r2 * ( cosα + isinα ) * ( cosβ + isinβ )
展开后面的乘式,得到
cosα * cosβ - sinα * sinβ + i( cosα * sinβ + sinα * cosβ )
根据三角函数公式,上面的式子就等于
cos(α+β) + isin(α+β)
所以,
( a + bi )( c + di ) = r1 * r2 * ( cos(α+β) + isin(α+β) )
这就证明了,两个复数相乘,就等于旋转半径相乘、旋转角度相加。
(完)


kmxz 说:
之前有一期《科学世界/Newton》上讲过这个话题,讲的很深入很好,建议有兴趣的可以找来看看
2012年9月25日 00:24 | # | 引用
honghu91 说:
从更抽象层次上来讲,只是数域的扩张的一种形态,实数域添加一个元素i扩张为复数域,可以添加任何一个不能用实数域线性表示的元素来扩张数域
2012年9月25日 01:12 | # | 引用
cfly 说:
向量 放到这些例子里也行吧
2012年9月25日 01:34 | # | 引用
Verbalist 说:
“虚数”这个名词是17世纪著名数学家、哲学家笛卡尔创制,因为当时的观念认为这是真实不存在的数字。后来发现虚数可对应平面上的纵轴,与对应平面上横轴的实数同样真实。
笛卡尔称“虚数”的本意就是指它是虚假的;莱布尼兹则认为:“虚数是美妙而奇异的神灵隐蔽所,它几乎是既存在又不存在的两栖物。”
(以上来自百度百科)
笛卡尔和莱布尼茨,这两位大陆理性派的哲学家都是独具源创性的天才。
虚数(和实数相垂直,垂直意味着对表示实在的维度的否定)使得二维平面的坐标系(这同样归功于笛卡尔)内在于原本只是一维的数的表达本身了。
2012年9月25日 02:02 | # | 引用
cttet 说:
还是觉得阮哥science方面的文章还是没有programming那么深入浅出了
虚数其实出来只是方便一些计算而已,在这里当然最好是要提一下向量了
2012年9月25日 03:25 | # | 引用
Sh4wnC 说:
"逆时针增加45度,相当于做了一个 1 + i 的变换。"
这是不对的,你把向量放大了。从你给的图上就能看出来,同样是一天的行驶,船开的更远了。
实际上应该乘以一个单位向量,所以你要把1+i单位化。变成sqrt(2)/2+i*sqrt(2)/2
2012年9月25日 06:28 | # | 引用
reverland 说:
后来看用旋转变量来解释复信号,才发现这都是基础啊……
2012年9月25日 07:31 | # | 引用
lukesun629 说:
中学教材应该引用这篇文章!
2012年9月25日 08:11 | # | 引用
;Xrong 说:
文章中有一点不大明白,为什么1+i表示旋转了45度啊?
2012年9月25日 08:22 | # | 引用
阮一峰 说:
太感谢了!这才意识到,我犯了大错。
现在已经改过了。
2012年9月25日 08:22 | # | 引用
阮一峰 说:
文章改过了,请刷新后,看修改后的提法。
2012年9月25日 08:23 | # | 引用
Xrong 说:
理解了,我觉得如果改成1 + 1i 会稍稍好理解一点
2012年9月25日 09:03 | # | 引用
CM 说:
还是不理解这个:
(+1) * (逆时针旋转90度) * (逆时针旋转90度) = (-1)
为什么连续2次旋转90度,是乘法关系,而不是加法关系
2012年9月25日 09:07 | # | 引用
t.k. 说:
好像很浅显易懂的样子。
2012年9月25日 09:13 | # | 引用
Si Wei 说:
1 × -1 = -1;
2012年9月25日 09:26 | # | 引用
自由国度 说:
感觉还是不对 为啥旋转90度是 90度×90度 而不是 90度+90度,换句话说,为啥公式是i^2=-1而不是2i=-1
2012年9月25日 09:28 | # | 引用
依云 说:
因为 i≠-1/2. 你乘以 -1 就是转个平角,那么转半个平角(一个直角)自然就是一半的「乘以-1」(而不是「乘以一半的 -1」)——也就是乘以 i 了。
2012年9月25日 09:37 | # | 引用
atlas 说:
这才是数学课本应该用的教材啊!
2012年9月25日 09:57 | # | 引用
closure 说:
过了这么多年,终于明白虚数的含义了。 不知道那些编教材的SB是干什么吃的。
2012年9月25日 12:51 | # | 引用
Alan haha 说:
推荐观看《维度:数学漫步》,好几年前的片子了= =里面介绍i就是旋转90°= =
2012年9月25日 13:10 | # | 引用
亭子 说:
非常喜欢您的文章,觉得通俗易懂,想请教您学习的方法和经常关注的网站。谢谢。
2012年9月25日 14:12 | # | 引用
guoqiao 说:
改了吗? 貌似我看到的还是不对的版本. 文章中都没有考虑复数的模, 只考虑了角度.
2012年9月25日 17:01 | # | 引用
Shadowmourne 说:
新课标高中教材就是这么讲的了……
2012年9月25日 17:10 | # | 引用
GeBron 说:
高中老师应该引用这篇文章,特别是一开始的 i 和“旋转”的关系。
2012年9月25日 17:36 | # | 引用
Henry 说:
我的理解是一维到二维的扩张,
类似的应该还有3维,aaa*1+bbb*i+ccc*j 这就是3维
2012年9月25日 20:11 | # | 引用
以地之名 说:
虚数实际上就是实数对,至少在数学分析中是这么定义的。
虚数乘法的定义是:(a,b)*(c,d)=(ac-bd,ad+bc)。这样,(0,1)*(0,1)=(-1,0)。相当于(0,1)是x^2=-1的一个解。
推荐Edmund Landau写的Foundations of Analysis。这本书介绍了如何从关于自然数的五条公理和若干简单事实出发构建整个数系。
2012年9月25日 20:33 | # | 引用
dirtyac 说:
我不是学数学的,不过你这说法有问题。实数系是有理运算闭合的了,不能再扩充。再扩充的话,就必须放弃某些性质(就是你说的自然数公理),比如复数的引入,就放弃了数“大小”的比较了。
2012年9月25日 21:29 | # | 引用
以地之名 说:
2012年9月25日 23:07 | # | 引用
堂哥 说:
哈哈,太有趣了,原来数学也不是那么枯燥乏味嘛,学校的教学方法有问题!
2012年9月26日 08:25 | # | 引用
rainliu 说:
i表示一个90°旋转,那1+i 为啥成了45°旋转呢?
2012年9月26日 15:15 | # | 引用
013231 说:
1 + i的角度就是45°. 同時它的長度是sqrt(2), 所以 * (1 + i)不僅轉了45°還延長爲原先的sqrt(2)倍.
2012年9月26日 16:18 | # | 引用
vcvbve 说:
2012年9月27日 13:12 | # | 引用
Elegant Tsai 说:
請問這圖是用什麼畫的啊??
2012年9月27日 20:10 | # | 引用
reverland 说:
从信息看应该是photoshop cs5 windows
2012年9月27日 20:17 | # | 引用
民科 说:
其实是用二维平面向量将旋转变换代数化,关键是复数的乘法
2012年9月28日 05:59 | # | 引用
xiaolic 说:
同意,这个片子让我搞懂了不少似是而非的东西,推荐~~
2012年9月28日 10:10 | # | 引用
凤凰鸟 说:
还是没讲清楚为什么用乘法来计算 1到-1的转变啊! 这样的话和直接记住 i= -1的平方没啥区别
2012年9月28日 13:50 | # | 引用
里沃特 说:
1+(-1)+(-1)=-1这个怎么解释。
为什么要 1*-1呢?
另外我觉得 1+i 代表 45度,只要我们把 i也看作 纵轴上的 1就容易弄懂了。
2012年9月28日 14:46 | # | 引用
mlyixi 说:
哈,以前只知道虚数是实数的二维扩充,方便处理问题用的.以前只理解了加法,看了文章原来还有乘法.
2012年9月28日 14:59 | # | 引用
agui5208 说:
看这篇就迷糊了,我还是功力尚浅啊
2012年9月28日 16:39 | # | 引用
王兴业 说:
2012年9月28日 18:06 | # | 引用
万俟尘 说:
挺想知道插图是用 Visio 还是什么做的?
2012年9月29日 00:08 | # | 引用
左岸读书 说:
越来越实用了。
2012年9月29日 00:19 | # | 引用
rodney 说:
一个实数就是一维直线上的点。虚数就是增加一维,成为平面上的点了。很久没琢磨数学问题了,不知道有没有人再增加一维,想过三维空间的点,1+i+j,再定义一下j和i之间的乘法加法运算,看看是否符合矢量合成定义?
2012年9月29日 08:23 | # | 引用
rodney 说:
另外想问一下,这篇文章里的图是用什么软件做的?效果很不错。
2012年9月29日 08:24 | # | 引用
鸟人100 说:
作为一个刚学虚数不久的高中生,看到这篇文章,本人深感庆幸。
2012年9月30日 21:52 | # | 引用
makefool 说:
自控原理险些不及格的飘过……如果那时候看过这篇文章,就不至于被那些鬼变换给弄得没有头脑了。
2012年9月30日 22:31 | # | 引用
dofine 说:
这里的乘法可以理解为广义的乘法, 类似群论的定义中的"乘法", 只是一种操作罢了.
2012年9月30日 23:24 | # | 引用
sicifus 说:
我觉得第一节就应该引入三角公式定理,
否则很难解释清楚为什么(逆时针旋转m+n度)=(逆时针旋转m度)*(逆时针旋转n度),而不是=(逆时针旋转m度)+(逆时针旋转n度),或者其他运算关系。
2012年10月 2日 09:13 | # | 引用
追逐好梦 说:
2012年10月 2日 10:02 | # | 引用
无敌豆腐干 说:
这个观点我是在数学漫步那个数学科普片里看到的,优酷上可以找到这个,推荐给大家看看
2012年10月 3日 15:05 | # | 引用
saint 说:
2012年10月 4日 21:33 | # | 引用
Platinum 说:
偶然看到这个,认为这篇解释得更好些(虽然都是用的相同的解释) http://jakwings.is-programmer.com/posts/29547.html
2012年10月 6日 01:09 | # | 引用
老N 说:
让我好好看,学的东西都还给老师了
2012年10月 6日 23:56 | # | 引用
木木老蔫 说:
文章很不错,评论非常精彩,顶了
2012年10月 9日 14:52 | # | 引用
iJay 说:
Matrix67上也聊过这个观点:http://www.matrix67.com/blog/archives/4294
2012年10月10日 19:30 | # | 引用
Timesand 说:
虚数在电工学里很有用的。
2012年10月11日 13:14 | # | 引用
arkodatta 说:
一下子清楚了很多,确实很精彩。
PS:评论里也说了1+i的模和角度的问题,好像文章还是没改过来。
2012年10月15日 19:12 | # | 引用
yasky 说:
方程x^2+1=0
在实数轴上是不成立的,也就是无根的。任何数自乘都是正数。但在平面上它可以成立,使它成立的那个对象记作i,不难看到这个i就是旋转90度的操作,两次i操作就能反向,所以在此意义下以上方程成立。i"数"开启了数学从对实数的算术运算进入到对更抽象的对象-向量进行运算的大门,从另一个角度看就是i扩充了数域。
2012年10月18日 09:52 | # | 引用
吴佳斌 说:
刚刚看到《从一到无穷大》中也有虚数的概念,在第二章,还有一个实例。
2012年10月20日 22:12 | # | 引用
袁源 说:
看完这篇,第一次发现原来我的大学数学学得还是很好的
2012年10月21日 22:34 | # | 引用
海纳百川 说:
多少年前的问题,到这里才算明白了一些。
2012年10月26日 16:35 | # | 引用
Sunnybreath 说:
其实您可以参考一下"希尔伯特变换"..这是在通信领域里很重要的一个变换式..
其实当把复数向"复平面"这种东西展开之后..诞生出来的"复变函数"便简化了很多三角运算..
对信号的处理基本上都离不开复变函数..因为要比"一维+一维"而叠合成的二维平面要方便得多..
2012年11月 7日 23:54 | # | 引用
helionacar 说:
刚在看关于运放闭环稳定性的问题,提到极点以及相位裕度的问题,看过你篇文章以后顿时觉得好理解多了
2012年12月13日 22:29 | # | 引用
绿豆 说:
虚数的运用只有维度辅助运算吗
2012年12月18日 13:51 | # | 引用
Krist 说:
我们的数学教育不太注重这种直观的理解。当年学高等代数的时候,老师从来不给我们讲一些理解性的东西,后来跳出繁杂的符号,认真领悟之后,运用得自如多了。
2012年12月27日 01:09 | # | 引用
een 说:
豆瓣 9.2 维度:数学漫步 Dimensions: A Walk Through Mathematics
里面有一节是讲复数,贴个视频网址如下
http://www.tudou.com/listplay/spNfryRD80k/iLWBrW0mCZk.html
不过对于数学专业,这样的理解太简单了,作为一个入门介绍则不错
2013年1月 9日 17:05 | # | 引用
杜函敏 说:
思路不错,但是这种证明有一个明显的问题,作者在进行旋转的时候,使用了乘法,但是复数的旋转不是复数定义的来源,是定义之后给出的性质。这种循环证明很难让人折服
2013年1月16日 00:08 | # | 引用
哇哈哈 说:
有點不明白,用"3+i"來表示一個力是什麽意思?物理上,力有兩個要素,大小和方向,是不是3是大小,i是方向,也就是第一張圖中偏離x軸的角度?
如果是這樣,那麼,3+i和1+3i這兩個力合成後,方向只能在i與3i之間才對啊,怎麼可能是4i呢?
2013年2月10日 22:52 | # | 引用
hayate 说:
2013年3月20日 09:59 | # | 引用
mll 说:
如果学校都是这种教学法,我肯定学习很好了,呵呵。
2013年3月27日 15:52 | # | 引用
V客小站 说:
受教了!又复习了一把数学。
2013年4月 1日 10:47 | # | 引用
robberM 说:
"数学家用一种特殊的表示方法,表示这个二维坐标:用 + 号把横坐标和纵坐标连接起来。比如,把 ( 1 , i ) 表示成 1 + i 。这种表示方法就叫做复数(complex number),其中 1 称为实数部,i 称为虚数部。"------我不太认同这里的说法。
比方说,在xoy坐标系,(3,4)表示x = 3,y = 4的点,3x + 4y 就表示从原点指向(3,4)的向量。在这里,横坐标是实数 1,纵坐标是虚数i,对应上去,这个可以叫做“1oi”坐标系。这样,1 + i就表示 在“1oi”坐标系内 由原点指向(1,1)点的向量,而且,它对应的点应该是(1,1),如果写成(1,i)就如同xoy坐标系内的(1,y)一样,是不对的。
2013年8月 5日 21:32 | # | 引用
sss 说:
1+i = (1,1*i)坐标为复平面上的(1,1),在45度线上
2013年9月 1日 15:00 | # | 引用
fortress 说:
最后的证明不太令人信服啊作者能够给出更有力的证明呢?
2013年10月11日 23:10 | # | 引用
kid 说:
对虚数的定义说的很清楚,不过还是没说明虚数的意义和实际用途,在几何中虚数并无多大意义,力学、地图学、航空学中才有比较实际应用意义
2013年10月18日 16:12 | # | 引用
GuoHneg 说:
为什么是“(+1) * (逆时针旋转90度) * (逆时针旋转90度) = (-1)”,而不是(+1) + (逆时针旋转90度) + (逆时针旋转90度) = (-1)
推到的这个地方写的不是很详细呀
2013年12月 3日 17:21 | # | 引用
Ariesfish 说:
相乘就相当于点在坐标空间旋转,比如1乘以-1相当于逆时针旋转180,所以用每逆时针旋转90度相当于乘一次(逆时针旋转90度)
2014年1月17日 21:14 | # | 引用
阿斯顿 说:
2014年1月24日 17:58 | # | 引用
孔超 说:
纠结了很久啊,终于明白了
2014年2月22日 16:31 | # | 引用
刘默飞 说:
那么方程中无实数解只有虚根,那里面虚根可以求么?怎么求?
2014年4月15日 14:18 | # | 引用
张先生 说:
向量存在,当两向量相乘存在COS夹角关系,当夹角为180度时
时出现负一关系,现实中作用力与反作用力就是这种情况,故X
*2有负一存在,这是数学对客观的表达,其它90度转两次是不对
的。
2014年5月 8日 13:27 | # | 引用
老屋 说:
(3,4)应该是3+4i,这里的i是定义出来的,不可以省略掉。
"数学家用一种特殊的表示方法,表示这个二维坐标:用 + 号把横坐标和纵坐标连接起来。比如,把 ( 1 , i ) 表示成 1 + i 。这种表示方法就叫做复数(complex number),其中 1 称为实数部,i 称为虚数部。"------我不太认同这里的说法。
比方说,在xoy坐标系,(3,4)表示x = 3,y = 4的点,3x + 4y 就表示从原点指向(3,4)的向量。在这里,横坐标是实数 1,纵坐标是虚数i,对应上去,这个可以叫做“1oi”坐标系。这样,1 + i就表示 在“1oi”坐标系内 由原点指向(1,1)点的向量,而且,它对应的点应该是(1,1),如果写成(1,i)就如同xoy坐标系内的(1,y)一样,是不对的。
2014年8月25日 21:20 | # | 引用
minsz 说:
我们对数的认识观念要不断更新,数不仅仅是算术量,它有可好位置对应,并可作运动变换。因此自然地我们必须挖掘工具,坐标,复数,向量,这些工具出现了。质点运动变化位置集合就是轨迹、图形,而运动变化方式常见特征,有平移,旋转,翻转,放大缩小,等等。
复数是一种旋转伸缩变换工具。这完全超出了算术量一维只可加性。
我们的狭隘,是由于我们认识的局限,无知。我们常常轻易去下超出我们认识水平的结论。
2014年12月 9日 09:14 | # | 引用
ZZpt 说:
我覺得學校教育有點競爭跟篩選的意味
有些老師不想教怎麼想,只丟一些結果(如果大家都不發問),某種程度是壞處,因為都看不懂,連定理都看不懂,更別說解題。
但是丟這種幫你把細節都填補好了,很優美,很順暢,甚至把背後的歷史脈絡,為什麼會發展出來,類似微積分這樣,老實講理解基本定理,只要你是智商100的人都ok。
但是這樣某種程度上,就類似台灣被罵的建構式教學,老實講就是學了分數會很高,然後那些同學一副很厲害的感覺(後來很強,跟天分無關,應該說老師很強)---情況一
大學有同學更絕,微積分沒學完,熱力學整個學完了,但是熱力學有些基本公式推導要用到幾個很基礎的微積分概念,我真的滿佩服他的填鴨功力.......前面不懂裝懂,一路學下去,根本考試神人-----情況二
如果學生完全不敢去自己假設,自己猜測,自己去跳躍,而是讓人在後面推,是可以比自己慢慢走的人快很多,但未必是好處---情況一
但是像是我這種資源或者小時候沒什麼刺激的學生,如果說一直卡在很簡單的一些定理,那也很痛苦,或者是像我同學囫圇吞棗,去不自知(不知道沒有思考的痛苦是幸運還是不幸)
把細節都抹掉,留下最後結構,國外大部分有極佳的科普書,還有科普教育,所以國外可能可行。
大學的數學系,常常都會有習題課,助教會教解題,不會說不懂只能自己想,基本上數學系這種教學才是正常的教學,會有很難的習題給你想,但是基本的習題不會,可以問助教等等。
但是國中高中,有些老師基本上都不管學生會不會,因為很多老師基本上沒本事,只是混飯吃(拿著碩士學歷,但是不願意教學,那請問他來當老師,不是代表他想混飯吃?),要是把學生教太厲害,整天問問題,他們就倒了。
所以我覺得在這種教學跟有點半填鴨教學要取得平衡,像是數學系那種有教概念,也有很多題目給學生動腦比較好。
2015年1月10日 17:00 | # | 引用
capewu 说:
貌似引入这个证明可以让不太熟悉旋转运算数学表示方法的同学更容易明白。
2015年2月26日 17:21 | # | 引用
pmst 说:
阮哥 文章更改过了吗? 为什么还是1+i,没有修改成单位向量吗
2015年3月27日 10:10 | # | 引用
罗隐 说:
你这个文章前面我懂,可后面我不懂,你能更详细吗?
2015年3月28日 14:19 | # | 引用
cjling 说:
虚数怎么看都像是二维向量的另一种表述,乘法就是内积,是不是当时还没有发明向量的概念,后面有了之后但由于历史习惯继续沿用了虚数?
2015年8月12日 12:20 | # | 引用
然也 说:
你说道:
我们可以知道,虚数 i 就是逆时针旋转90度,i 不是一个数,而是一个旋转量。
二、复数的定义
既然 i 表示旋转量,我们就可以用 i ,表示任何实数的旋转状态。
将实数轴看作横轴,虚数轴看作纵轴,就构成了一个二维平面。旋转到某一个角度的任何正实数,必然唯一对应这个平面中的某个点。只要确定横坐标和纵坐标,比如( 1 , i ),就可以确定某个实数的旋转量(45度)。
【不是说“i是一个旋转量,i 就是逆时针旋转90度”吗?在( 1 , i )中,i怎么又不是“旋转量”,而成了“纵轴”上的一个点呢?如果说“i是一个旋转量,i 就是逆时针旋转90度”。那么“1 + i”应该是“1 + 逆时针旋转90度”。现在“1 + i”怎么又成了45度?如果说“i是一个旋转量,i 就是逆时针旋转90度”,那么45度为什么不能用 i/2 来表示?】
你还说道;
数学家用一种特殊的表示方法,表示这个二维坐标:用 + 号把横坐标和纵坐标连接起来。比如,把 ( 1 , i ) 表示成 1 + i 。这种表示方法就叫做复数(complex number),其中 1 称为实数部,i 称为虚数部。
为什么要把二维坐标表示成这样呢,下一节告诉你原因。
三、虚数的作用:加法
虚数的引入,大大方便了涉及到旋转的计算。
比如,物理学需要计算"力的合成"。假定一个力是 3 + i ,另一个力是 1 + 3i ,请问它们的合成力是多少?
根据"平行四边形法则",你马上得到,合成力就是 ( 3 + i ) + ( 1 + 3i ) = ( 4 + 4i )。
这就是虚数加法的物理意义。
【在这里,如果我们不用i= (-1)^1/2 这种“概念”,而是直接使用点的坐标的相加,——比如,物理学需要计算"力的合成"。假定一个力是(3 ,1) ,另一个力是 (1,3) ,请问它们的合成力是多少?根据"平行四边形法则",你马上得到,合成力就是(3 ,1) + (1,3) = ( 4,4) —— 行吗?】
四、虚数的作用:乘法
如果涉及到旋转角度的改变,处理起来更方便。
比如,一条船的航向是 3 + 4i 。
如果该船的航向,逆时针增加45度,请问新航向是多少?
45度的航向就是 1 + i 。计算新航向,只要把这两个航向 3 + 4i 与 1 + i 相乘就可以了(原因在下一节解释):
( 3 + 4i ) * ( 1 + i ) = ( -1 + 7i )
所以,该船的新航向是 -1 + 7i 。【如果已知“老航向的角度”,那么直接在“老航向的角度”上加上45度不是更省事?】
2015年11月 3日 10:09 | # | 引用
然也 说:
四、虚数的作用:乘法
如果涉及到旋转角度的改变,处理起来更方便。
比如,一条船的航向是 3 + 4i 。
如果该船的航向,逆时针增加45度,请问新航向是多少?
45度的航向就是 1 + i 。计算新航向,只要把这两个航向 3 + 4i 与 1 + i 相乘就可以了(原因在下一节解释):
( 3 + 4i ) * ( 1 + i ) = ( -1 + 7i )
所以,该船的新航向是 -1 + 7i 。
【如果已知“老航向的角度”,那么直接在“老航向的角度”上加上45度是不是更省事?】
2015年11月 3日 10:13 | # | 引用
123 说:
只是说方向
2015年11月11日 11:30 | # | 引用
CycleUser 说:
模长单位化确实现在刷新的还是旧版本的,就是还是1+i。
个人认为作为向量来理解是最方便的一种解决方式,而且乘法加法等等也都更好理解了。
再者,关于教材,我始终认为,优秀的人需要有足够的探索精神,起码要对教材以外而自己感觉好奇的内容能够进行独立的学习。一切都靠教材是不现实的,完美的教材也是难以实现的。自己多动脑,多探索,多学习,如此而已。
比如Ramanujan就是一个很好的例子,如果只天天期盼更精致的教材,恐怕难以有太大成就了。
天天指望别人给修桥铺路的人,怎么能走得了徐霞客的旅途呢?
2015年11月16日 23:01 | # | 引用
iMusicDog 说:
你那样得不到相对原点的方向。
2015年12月21日 17:02 | # | 引用
Ltre 说:
直接从+1变为-1,那么可以作 1 * -1 = -1 计算;但如果硬要乘两次、且每次都乘得一样,那么可以考虑乘数为sqrt(-1),在坐标图中,Y轴正向+1点处可作为不错的落点选择。
2016年2月27日 00:59 | # | 引用
jesse 说:
这个地方确实没有说清楚,我也困惑了很久,这样解释:为什么是乘法而不是加法?因为如果是+,那么
(+1) * (逆时针旋转90度) + (+1) * (逆时针旋转90度) = 2 * (+1) * (逆时针旋转90度),实际上,在第一次转完90度后,并没有再次旋转,而是向转完90度的新方向上 继续跑了一个单位长度(得到-2i),或者可以认为是单位2转了90度,所以,不能等价于单位1转完180度,如果要单位1转180度,以90度为一次,转一次*(逆时针旋转90度),再转一次,就必然是再*(逆时针旋转90度),因为是再转一次,而不是转完一次后停住,然后执行其他动作。
2016年5月17日 14:50 | # | 引用
老蛤 说:
旋转为什么是乘法法则??
2016年7月21日 21:07 | # | 引用
怪蜀黎 说:
一圈是 +1
半圈是 -1
以此类推,某数学家就把半半圈(90度)虚构de设定为 ✓-1(这个虚构出来的数其实就是相对值或基准值) ,
因此 ✓-1 * ✓-1 = -1 ,
那么4/3圈是 ✓-1 * ✓-1 * ✓-1 = -✓-1,
4/4圈是 ✓-1 * ✓-1 * ✓-1 * ✓-1 = 1
零圈是 ✓-1 / ✓-1 = 1
因“半半圈是✓-1”是虚构出来的所以称做虚数(按中文),并标记它为i。。。。
更多内容可以去YOUTUBE搜“维度:数学漫步”
2016年12月26日 15:57 | # | 引用
jindongdong 说:
旋转45度,用1+i确实不对,应该保证单位模,所以需要除以√2/2。貌似阮哥也发现这个问题了,但不知为什么没有改过来。
2017年3月15日 20:23 | # | 引用
王灵通 说:
上高中时我的数学并不好,也是后来阅读大量的向量文献才弄懂的,旋转也是向量,那么向量的三角形法则、平行四边形法则及向量乘法这种古怪的运算方法又是为什么呢?其实它只是一个数学模型。知道向量大小为什么叫模长了吧!旋转遵循向量思想,也就是一个数学模型,不能用纯数学推理得到答案,说白了叫规定。因此是1×90度×90度=-1而不是连加,旋转命题既有推理又有规定。图形只是物理范畴,而旋转命题是数学,平方不是简单的相加,根号下也不是简单的分离,希望能帮助你们解决为什么是相乘而不是相加的困惑。
2017年8月17日 13:49 | # | 引用
欧丁 说:
显然,逆时针旋转180度,+1就会变成-1。
并不显然,就像地球的旋转,并没有使黄种人晚上变成黑种人。我觉得通过旋转把1变成-1,这和规定i^2=-1,没啥区别,还是人为的规定而已,或者说小把戏。
2017年8月24日 15:48 | # | 引用
LQA 说:
雖然剛上高中不久,但還是有點明白的。
那麼函數y=x^2+1也能在某個座標軸上表達出它的虛數解了?
2017年10月15日 22:19 | # | 引用
Imcodingcc 说:
时间陡然回到了初中时期。
2017年11月 9日 21:14 | # | 引用
二十画生 说:
非常棒!
其实早在此文之前,我有幸看过北航教授的公开课,里面就指出了i作为旋转度的含义,其时,也是备受启发,非常惊讶,反反复复看了好多遍!
北航数学大观:http://open.163.com/special/cuvocw/shuxuedaguan.html
2018年2月11日 11:17 | # | 引用
鶸 说:
感谢博主,通俗易懂。(虽然弄懂花了挺久的)
2018年4月23日 23:43 | # | 引用
calvin 说:
阮哥一定没看过《从一到无穷大》,里面写的很清楚
2018年8月10日 00:47 | # | 引用
CarlKang 说:
在复数坐标系中标出下列复数,问复数乘以i的几何意义?
3+4i, (3+4i)i,(3+4i)i*i,(3+4i)i*i*i,(3+4i)i*i*i*i。
2018年9月19日 04:35 | # | 引用
Edward 说:
胡说八道
2019年11月28日 09:23 | # | 引用
飞霜儿 说:
前段时间因为看了部《追缉炸弹客》,好奇心犯了,对真实的卡辛斯基编写的《论工业社会及其未来》的原文细细读了好几遍,然而也从网上看到您的网络日志,顿时感慨,不得不说,从小时候读过鲁迅的朝花夕拾到得知他弃医从文的执念,文字对人的内心的共鸣,冲击力是真的很大。有时会反思自己是不是被这个社会给思想禁锢了,麻木的活着,不思考不听从内心的声音,反而活在无知无畏的牢笼里。所以您的文集里,我有闲暇时也登陆看看,好奇着,你的思维可以那么敏锐,你的文笔能表达你心底里的话。不管如何,字里行间,总有产生共鸣的感触。
2019年11月28日 12:02 | # | 引用
fangzhu2000 说:
“比如,一条船的航向是 3 + 4i 。
如果该船的航向,逆时针增加45度,请问新航向是多少?”
请改成:比如,一条船的航行状态是:3 + 4i。。。。。。。。
因为3+4i表达的是向量,不光有航向,还有速度的表达。
2019年12月13日 11:33 | # | 引用
刘齐 说:
数学的抽象性和直观性是其双翼,数学的普适性和深刻性是其灵魂。虚数首先是数学需要的抽象定义,如同1为实数单位,i为虚数单位,解释为1向左转九十度给出了其直观含义,加深了虚数单位的理解。点赞!
2020年1月16日 18:23 | # | 引用
荒野小哥哥 说:
因为本来就是乘法哦。当时人们思索什么数的平方等于-1呢?也即:
I2= -1 也即: 1 × I × I = -1 //这里为区分乘号,通常示例的未知数X替换为I吧
可能大家更习惯代数式形式化表示,阮大这里直接用文字,所以让不少人费解了。
2020年3月 3日 12:27 | # | 引用
max 说:
听了您的讲解,豁然开朗!感谢,有的知识点高中的时候老视根本没讲过
2020年4月25日 12:48 | # | 引用
xdsnet 说:
确实前面说的1+i并不是仅仅逆时针旋转45度,而是逆时针旋转45度,并加速倍数为sqrt(2)
正确的只逆时针旋转45度应该是(sqrt(2)/2 + sqrt(2)i/2) 这样一个量。
2020年6月 4日 10:19 | # | 引用
Cris yang 说:
还不懂得可以去看看欧拉公式
2020年11月16日 11:47 | # | 引用
aihao 说:
实数向左旋转90度是实数*i,那1左旋45度等于根号i吗?何必非用复数表示?
2022年1月 2日 17:07 | # | 引用
daby 说:
复数都讲了,大大能不能讲下四元数,这个太难理解了,找了好多博客资料还是看不懂
2022年2月28日 01:21 | # | 引用
james 说:
所以这解释只是避开问题不谈,并没有解开任何疑惑。开篇那个1乘旋转乘旋转就是错的,说白了就是强行凑个形式逼你相信。i代表旋转更是无稽之谈,这只是在这里那它这么用罢了,在别的应用领域旋转的含义荡然无存
2022年5月 5日 03:58 | # | 引用
void6 说:
挺通俗易懂的解釋,謝謝。感覺很多數學問題移到三維甚至多維角度去思考就能找到答案,很神奇。
2022年10月 3日 02:23 | # | 引用
Fermi 说:
我觉得虚数就是凭空从虚空中借了一位数,然后再还回去。就像你用21减9,个位上的1会向十位的2借一位数。这个图解中多出来的纵轴既不属于一维平面也不属于二维平面,就是虚拟一个出来一个纬度。
在数学中,虚数与四维空间有一种数不清也道不明的关系。虚数就像是虫洞,降维解决了三维上的问题。
这个问题也是我想了很久,知道了解黎曼猜想和广义相对论以后。
2022年11月15日 04:10 | # | 引用