本文通过五个例子,介绍蒙特卡罗方法(Monte Carlo Method)。

一、概述
蒙特卡罗方法是一种计算方法。原理是通过大量随机样本,去了解一个系统,进而得到所要计算的值。
它非常强大和灵活,又相当简单易懂,很容易实现。对于许多问题来说,它往往是最简单的计算方法,有时甚至是唯一可行的方法。

它诞生于上个世纪40年代美国的"曼哈顿计划",名字来源于赌城蒙特卡罗,象征概率。
二、π的计算
第一个例子是,如何用蒙特卡罗方法计算圆周率π。
正方形内部有一个相切的圆,它们的面积之比是π/4。
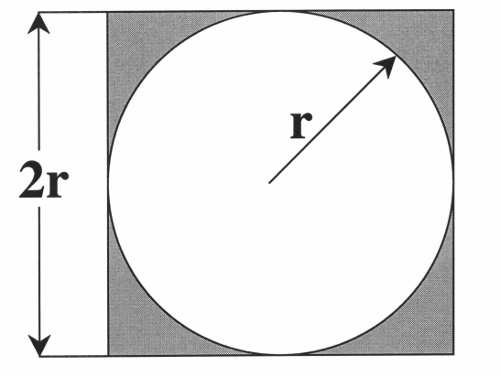
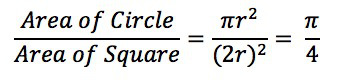
现在,在这个正方形内部,随机产生10000个点(即10000个坐标对 (x, y)),计算它们与中心点的距离,从而判断是否落在圆的内部。

如果这些点均匀分布,那么圆内的点应该占到所有点的 π/4,因此将这个比值乘以4,就是π的值。通过R语言脚本随机模拟30000个点,π的估算值与真实值相差0.07%。
三、积分的计算
上面的方法加以推广,就可以计算任意一个积分的值。
比如,计算函数 y = x2 在 [0, 1] 区间的积分,就是求出下图红色部分的面积。
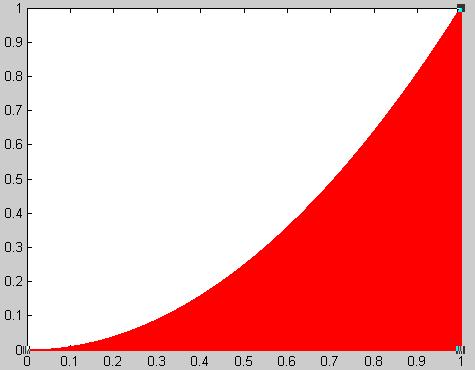
这个函数在 (1,1) 点的取值为1,所以整个红色区域在一个面积为1的正方形里面。在该正方形内部,产生大量随机点,可以计算出有多少点落在红色区域(判断条件 y < x2)。这个比重就是所要求的积分值。
用Matlab模拟100万个随机点,结果为0.3328。
四、交通堵塞
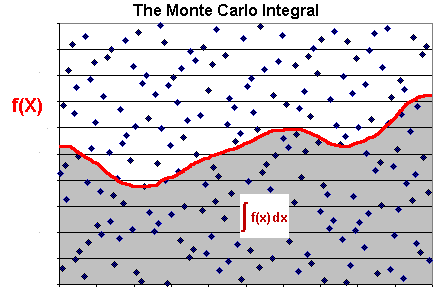
蒙特卡罗方法不仅可以用于计算,还可以用于模拟系统内部的随机运动。下面的例子模拟单车道的交通堵塞。
根据 Nagel-Schreckenberg 模型,车辆的运动满足以下规则。
- 当前速度是 v 。
- 如果前面没车,它在下一秒的速度会提高到 v + 1 ,直到达到规定的最高限速。
- 如果前面有车,距离为d,且 d < v,那么它在下一秒的速度会降低到 d - 1 。
- 此外,司机还会以概率 p 随机减速, 将下一秒的速度降低到 v - 1 。
在一条直线上,随机产生100个点,代表道路上的100辆车,另取概率 p 为 0.3 。
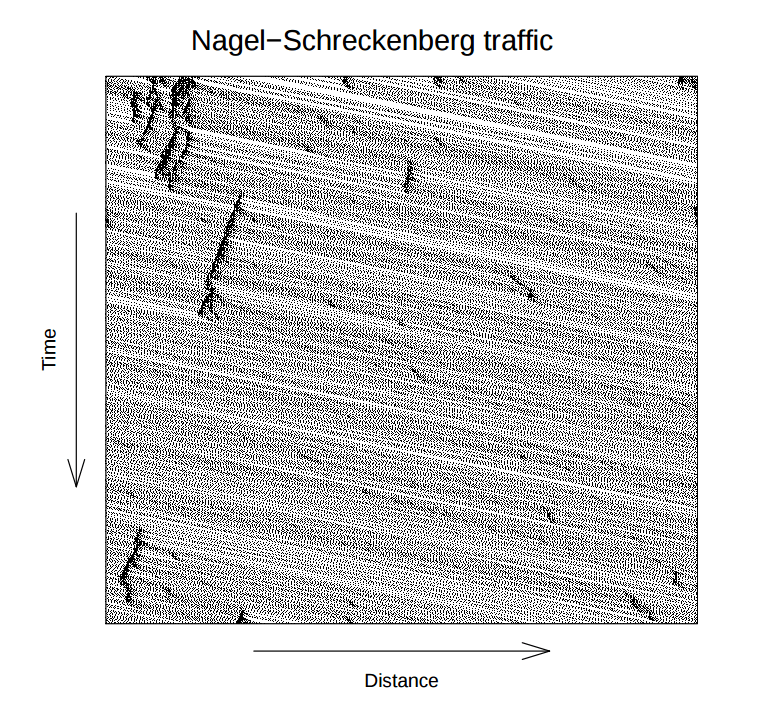
上图中,横轴代表距离(从左到右),纵轴代表时间(从上到下),因此每一行就表示下一秒的道路情况。
可以看到,该模型会随机产生交通拥堵(图形上黑色聚集的部分)。这就证明了,单车道即使没有任何原因,也会产生交通堵塞。
五、产品厚度
某产品由八个零件堆叠组成。也就是说,这八个零件的厚度总和,等于该产品的厚度。
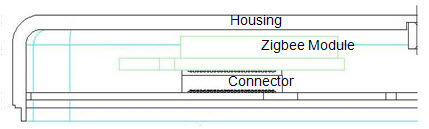
已知该产品的厚度,必须控制在27mm以内,但是每个零件有一定的概率,厚度会超出误差。请问有多大的概率,产品的厚度会超出27mm?
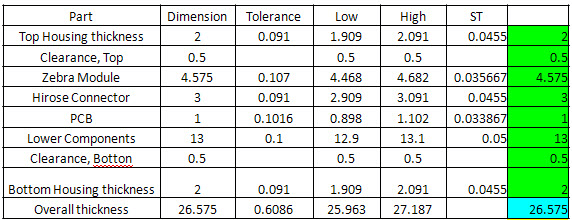
取100000个随机样本,每个样本有8个值,对应8个零件各自的厚度。计算发现,产品的合格率为99.9979%,即百万分之21的概率,厚度会超出27mm。
六、证券市场
证券市场有时交易活跃,有时交易冷清。下面是你对市场的预测。
- 如果交易冷清,你会以平均价11元,卖出5万股。
- 如果交易活跃,你会以平均价8元,卖出10万股。
- 如果交易温和,你会以平均价10元,卖出7.5万股。
已知你的成本在每股5.5元到7.5元之间,平均是6.5元。请问接下来的交易,你的净利润会是多少?
取1000个随机样本,每个样本有两个数值:一个是证券的成本(5.5元到7.5元之间的均匀分布),另一个是当前市场状态(冷清、活跃、温和,各有三分之一可能)。
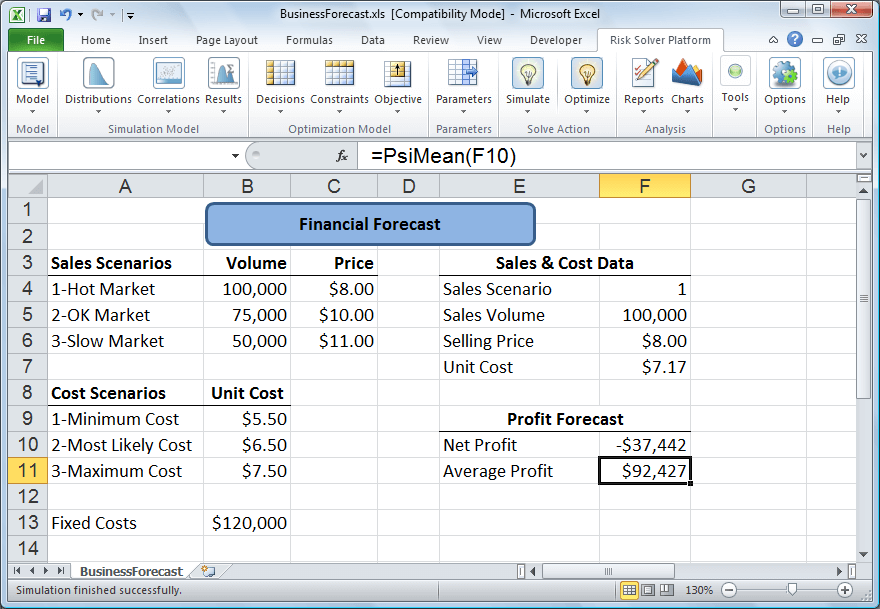
模拟计算得到,平均净利润为92, 427美元。
七,参考链接
- Introduction To Monte Carlo Methods,by Alex Woods
- Monte Carlo Simulation Tutorial
- 蒙特卡罗(Monte Carlo)方法简介,by 王晓勇
- 蒙特卡罗(Monte Carlo)模拟的一个应用实例
(完)


John 说:
文中的蒙特卡罗太狭窄了...
随机算法分为两类
蒙特卡罗和拉斯维加斯
蒙特卡罗指的是算法的时间复杂度固定,然而结果有一定几率失败
拉斯维加斯指的是算法一定成功,然而运行时间是概率的
拉斯维加斯比较好的例子有:quicksort,quickselect,skip list等
文中的取样随机变量只是蒙特卡罗算法的一小部分,更准确地说是PRAS(Polynomial-time Randomized Approximation Scheme)
我希望以较大概率得到一个误差率在1/epsilon范围内的值,于是用O(p(n)epsilon)的复杂度去计算,大概是这种感觉。
其他的蒙特卡罗可以做到最优化或者判定性问题,例如7/8估计Max3SAT问题的算法
给定一个Max3SAT实例,算法随机给每个变量赋值,重复很多次取最优解
可以证明有较大概率得到一个最优解7/8以上的解(Tardos的书上应该有证明)
其实注意到所有的拉斯维加斯算法都可以转化为蒙特卡罗算法,反之不一定,很多时候会直接研究蒙特卡罗算法
2015年7月27日 15:13 | # | 引用
drunkevil 说:
文中的例子有点过于简单,倒是跟标题很一致。
2015年7月27日 15:47 | # | 引用
helen 说:
请问一下,您在博客里的画的图是用啥工具画的啊?我常看您的博客,觉得你的博客图片很多,给我带来了很多形象的理解。感谢!
2015年7月27日 17:14 | # | 引用
Lutz 说:
我认为博主这篇文章并没打算涉及任何算法层面的内容,只是在用一种形象的方式介绍蒙特卡罗方法的中心思想。
本文第一句话中有个Monte Carlo method的wiki链接,如果您有点进去看过的话,应该很容易发现,那篇wiki的第一句话就是:Not to be confused with Monte Carlo algorithm.
2015年7月27日 19:44 | # | 引用
flag_H 说:
讲蒙特卡罗模拟的用途,至于蒙特卡罗如何计算,都有软件。比如证券这个例子,1000次抽样,每次按均匀分布随机选定一个成本值、同时按1/3的概率选中一个市场情境,然后拿这两个参数可计算出净利润、平均利润,千次加总并取均值就是结果。1000次抽样的技术本身就是蒙特卡罗模拟,这个作者没讲,也没必要讲,毕竟,本文只是在介绍蒙特卡罗模拟的用途。
2015年7月27日 23:11 | # | 引用
芬兰湾 说:
小时候在课外书上学过一个计算 pi 值的算法,用一根长度为 2r 的小木棍,随机地丢在行间距为 r 的信纸上(就是那种很常见的一行一行的信纸),然后数木棍和线的交叉点,然后除以丢的次数,就可以得到 pi 的近似值,当时觉得很神奇,用的应该就是本文介绍的方法。
2015年7月28日 11:27 | # | 引用
bigTom 说:
学习了,动手算了下,感觉证券市场那题算错了,求指导
#-*-coding:utf-8-*-
import random
def countProfit(n):
count = 0;
for i in range(n):
cost = random.uniform(5.5,7.5)
pro = (11 - cost)*5 + (8 - cost)*10 + (10 - cost)*7.5
count += pro;
return count / (3*n)
print countProfit(400)
我算了21万多额,求指导
2015年7月28日 23:24 | # | 引用
ooxx 说:
我用py和c各编了一个,每次计算都在 3.7 ,误差太大了
我的方法是取一组两个0-1的随机数,(x,y),在第一象限,四分之一圆弧,面积为pi*1*1/4,正方形面积为1*1,比值也是pi/4
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from random import random
from math import sqrt
x = y = inn = out = 0.0
for i in range(30000):
x = random()
y = random()
print(x, y)
if (sqrt(x * x + y * y) inn += 1.0
else:
out += 1.0
print(inn / out)
2015年7月29日 15:21 | # | 引用
bigTom 说:
@ooxx:
你这个确实有问题,不是均匀分布吧,要用random.uniform(),才是均匀分布
2015年7月29日 22:22 | # | 引用
liaotonglang 说:
学算法的时候树上的蒙特卡罗算法只讲了计算圆周率的例子,我以为那就是蒙特卡罗的全部内容呢。现在才恍然大悟。
2015年7月30日 09:08 | # | 引用
liaotonglang 说:
看样子不是很难。之前做过一个系统仿真程序,原来那就是蒙特卡罗算法。
2015年7月30日 09:11 | # | 引用
lpm 说:
07年开始订阅你的Blog,到现在,以及将来...每篇必读
近几年工作上遇到些情况,需要转化数学概念为生产力。
从开始把分类里的每篇文章看了又看.写的太棒!篇篇精品!
2015年7月31日 13:15 | # | 引用
jqk6 说:
没看明白这个方法,能否画个图?
2015年7月31日 14:29 | # | 引用
David Aldrich 说:
这是布丰投针实验,在概率论的发展史上很有名。用简单的几何概型知识可以知道,如果将一个半径为r/pi的圆随机地丢在行间距为r的一组数目足够多的等距平行线之间,则圆与平行线有公共点的概率为2/pi。布丰的想法,可以简单地理解为,布丰认为将这个圆从中间剪开,拉直为一个线段之后,这条线段与平行线有2个公共点的概率不变,仍为2/pi。易知,这条线段的长度为2r。进行大量的“投针”实验后,这条线段与平行线有公共点的概率可以近似地认为等于实验中线段与平行线有公共点的次数除以总的投针次数。简单的运算之后,大家就可以知道,总的投针次数除以实验中线段与平行线有公共点的次数的结果即为pi/2的近似值。
2015年8月 1日 18:44 | # | 引用
清华研读间 说:
您好,我是微信公共平台“清华研读间”(ID:qinghuayandujian)的学生编辑,我们平台由清华大学研究生团委主办,读者大部分为清华本校研究生、本科生和关注清华的社会人士。
现在想申请《蒙特卡罗方法入门》一文的转载授权,希望将此文转载于我们的公共平台上,让更多的人阅读到好文章。
盼回复。
2015年8月 6日 09:28 | # | 引用
路过不要错过 说:
就算是用UNIFORM很难算到3.1******
2015年8月 7日 23:13 | # | 引用
assassindesign 说:
@bigTom:
注意有个固定支出成本fixed costs=$120000 最后结果减去这个数就对了 ,这个文章也是站长自己找的资料,他翻译的时候忽略了
2015年8月 7日 23:51 | # | 引用
freeman 说:
最后一个excel表中的内容没看明白,谁能解释一下。
多谢!
2015年8月19日 18:37 | # | 引用
eric_xu 说:
是的(4.5*5+1.5*10+3.5*7.5)/3-12 = 9.25(万) 必须有个12万才对。
2015年8月26日 11:58 | # | 引用
cococ 说:
学习了!!!收藏!
2015年8月27日 00:39 | # | 引用
余初河 说:
交通拥堵那个例子,貌似和蒙特卡洛没有太大关系吧?NaSch模型仿真用的是元胞自动机模型,随机刹车概率是固定的p。
2015年9月17日 16:40 | # | 引用
test 说:
这个明显是代码写错了, inn应该是去除总数30000再乘以4才是pi
2015年9月22日 11:44 | # | 引用
nononono 说:
应该是 print(4*inn/30000)
2015年10月31日 03:06 | # | 引用
lambdalpha 说:
import numpy as np
import random
n = 10000
r = 1.0
data = [random.random()**2 + random.random()**2 for x in range(n)]
num = np.sum(np.array(data) < r**2)
p = 4.0 * num / n
print("pi is roughly: " , p)
2015年11月19日 15:17 | # | 引用
bestwish 说:
2015年12月 8日 17:51 | # | 引用
Iaoo 说:
正方形与圆的比是 4/π 才对啊!
2016年1月31日 02:30 | # | 引用
wbb 说:
感谢分享,真的很有用。
2016年2月 5日 09:27 | # | 引用
qinyang1104 说:
用random()函数没错。
最后一句print(inn / out)错了。
改成:print(inn / (out + inn) * 4)
2016年3月30日 15:02 | # | 引用
ldb 说:
有个问题,为什么要随机。如果换成点阵式的排列会不会更精准一些?
2016年8月19日 15:48 | # | 引用
大河小鱼 说:
若用点阵,虽然均匀,但由于点间距必须是固定的,人为地影响了圆周附近部分点是否在圆内,因此这个固定的点间距会对计算结果产生影响。因此若要减小误差,就得不断提高点阵密度,所需计算量/工作量要大一些(个人认为)。
若采用随机点,相当于任意精度的点阵,消除了固定间距的影响,因此可以用更少的点取得差不多的结果。
2016年9月 1日 10:53 | # | 引用
dafuh 说:
@David Aldrich:
你所说的概率2/pi并不是这么简单得来的。建议大家不妨查阅其它更为详细的资料。
2016年9月 1日 13:53 | # | 引用
chun 说:
用Matlab模拟了一下
num = 100000;
x = rand(num, 1);
sim_y = rand(num, 1);
eval('y = x.^2;');
area = sum(sim_y
plot_x = 0:0.01:1;
plot_y = plot_x.^2;
plot(x, sim_y, '.');
hold on;
plot(plot_x, plot_y, 'linewidth', 2);
fprintf('area is %d', area);
10万个点,结果是0.3332500
2017年1月14日 11:12 | # | 引用
混吃等死 说:
可能你说得对,但是对于初学者来说,简单的几个例子,让人能快速理解蒙特卡洛是做什么的、怎么做的,我觉得很棒!
2017年8月25日 09:55 | # | 引用
王念一 说:
@John:
文章名叫『蒙特卡罗方法入门』,不叫『随机算法入门』
2018年2月10日 20:47 | # | 引用