1.
前几天,我在读一本C语言教材,有一道例题:
#include <stdio.h>
void main(void){
int num=9; /* num是整型变量,设为9 */
float* pFloat=# /* pFloat表示num的内存地址,但是设为浮点数 */
printf("num的值为:%d\n",num); /* 显示num的整型值 */
printf("*pFloat的值为:%f\n",*pFloat); /* 显示num的浮点值 */
*pFloat=9.0; /* 将num的值改为浮点数 */
printf("num的值为:%d\n",num); /* 显示num的整型值 */
printf("*pFloat的值为:%f\n",*pFloat); /* 显示num的浮点值 */
}
运行结果如下:
num的值为:9
*pFloat的值为:0.000000
num的值为:1091567616
*pFloat的值为:9.000000
我很惊讶,num和*pFloat在内存中明明是同一个数,为什么浮点数和整数的解读结果会差别这么大?
要理解这个结果,一定要搞懂浮点数在计算机内部的表示方法。我读了一些资料,下面就是我的笔记。
2.
在讨论浮点数之前,先看一下整数在计算机内部是怎样表示的。
int num=9;
上面这条命令,声明了一个整数变量,类型为int,值为9(二进制写法为1001)。普通的32位计算机,用4个字节表示int变量,所以9就被保存为00000000 00000000 00000000 00001001,写成16进制就是0x00000009。
那么,我们的问题就简化成:为什么0x00000009还原成浮点数,就成了0.000000?
3.
根据国际标准IEEE 754,任意一个二进制浮点数V可以表示成下面的形式:
(1)(-1)^s表示符号位,当s=0,V为正数;当s=1,V为负数。
(2)M表示有效数字,大于等于1,小于2。
(3)2^E表示指数位。
举例来说,十进制的5.0,写成二进制是101.0,相当于1.01×2^2。那么,按照上面V的格式,可以得出s=0,M=1.01,E=2。
十进制的-5.0,写成二进制是-101.0,相当于-1.01×2^2。那么,s=1,M=1.01,E=2。
IEEE 754规定,对于32位的浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M。
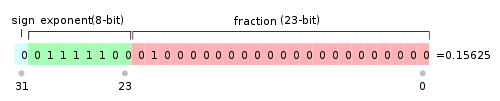
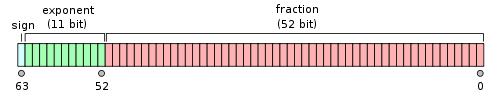
对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。
5.
IEEE 754对有效数字M和指数E,还有一些特别规定。
前面说过,1≤M<2,也就是说,M可以写成1.xxxxxx的形式,其中xxxxxx表示小数部分。IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂。
首先,E为一个无符号整数(unsigned int)。这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,E的真实值必须再减去一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。
比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
然后,指数E还可以再分成三种情况:
(1)E不全为0或不全为1。这时,浮点数就采用上面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第一位的1。
(2)E全为0。这时,浮点数的指数E等于1-127(或者1-1023),有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
(3)E全为1。这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);如果有效数字M不全为0,表示这个数不是一个数(NaN)。
6.
好了,关于浮点数的表示规则,就说到这里。
下面,让我们回到一开始的问题:为什么0x00000009还原成浮点数,就成了0.000000?
首先,将0x00000009拆分,得到第一位符号位s=0,后面8位的指数E=00000000,最后23位的有效数字M=000 0000 0000 0000 0000 1001。
由于指数E全为0,所以符合上一节的第二种情况。因此,浮点数V就写成:
V=(-1)^0×0.00000000000000000001001×2^(-126)=1.001×2^(-146)
显然,V是一个很小的接近于0的正数,所以用十进制小数表示就是0.000000。
7.
再看例题的第二部分。
请问浮点数9.0,如何用二进制表示?还原成十进制又是多少?
首先,浮点数9.0等于二进制的1001.0,即1.001×2^3。
那么,第一位的符号位s=0,有效数字M等于001后面再加20个0,凑满23位,指数E等于3+127=130,即10000010。
所以,写成二进制形式,应该是s+E+M,即0 10000010 001 0000 0000 0000 0000 0000。这个32位的二进制数,还原成十进制,正是1091567616。
(完)


半就业 说:
博主以前没有学过C语言??
2010年6月 6日 15:05 | # | 引用
许通 说:
研究得如此透彻。。。我是大二得学生,以前也学过C语言,但觉得学得不够好,现正在从头看《C Primer Plus》.博主看的是哪一本教材呢?
2010年6月 6日 15:30 | # | 引用
ddd 说:
我觉得研究这个细节真没有什么用。
2010年6月 6日 16:36 | # | 引用
许通 说:
不同意你的看法,我觉得研究这些细节有助于加深对C语言本质的理解。
2010年6月 6日 17:34 | # | 引用
幻の上帝 说:
除了涉及到C语言关键字float以外,这个真的和语言本身毛关系都没有。什么叫“C语言的本质”?
用什么方法实现浮点数运算,输入输出的细节,都是语言实现和语言用户的事情。
2010年6月 6日 18:17 | # | 引用
睦 说:
資料在檔案讀取,或運算後可能發生的錯誤都很難以除錯,經過博主的說明,更加清楚二者型別間轉換的差異,果然魔鬼就藏在細節裡,謝謝您的分享~ :)
2010年6月 6日 19:05 | # | 引用
z 说:
非科班的啊~
2010年6月 6日 21:58 | # | 引用
cc 说:
学到东西了,Thanks
2010年6月 6日 22:28 | # | 引用
Ruan YiFeng 说:
我以前自学过,好多地方看不懂。现在正好重新温习一遍。
2010年6月 6日 22:42 | # | 引用
Ruan YiFeng 说:
我现在看的是一本国产教材,随手从图书馆里拿的,就不说是哪一本了。
但是,我的这篇文章,很大部分出自《深入理解计算机系统》(Computer Systems: A Programmer Perspective)的第二章。
2010年6月 6日 22:46 | # | 引用
凌风 说:
这些在大学计算机专业的教材上都有讲的,比如《计算机组成原理》。
不是很难,有兴趣的大家可以去看看。
博主是非科班的,不简单啊,毕竟是术业有专攻嘛。
无意中在网上看到了你写的《如何变得有思想?》,过来逛逛。
2010年6月 6日 23:39 | # | 引用
roy_hu 说:
真要搞清楚,推荐What Every Computer Scientist Should Know About Floating-Point Arithmetic
2010年6月 6日 23:55 | # | 引用
鳞 说:
这行:
float* pFloat=# /* pFloat表示num的内存地址,但是设为浮点数 */
--
GCC编译器编译不过去的.
error: cannot convert 'int*' to 'float*' in initialization|
2010年6月 7日 08:58 | # | 引用
半就业 说:
2010年6月 7日 09:33 | # | 引用
半就业 说:
这个可是相当有用。明白了这个你就知道为什么整型变量可以通过移位来进行乘除法了,当然,还有很多技巧与此有关。
2010年6月 7日 09:49 | # | 引用
Ruan YiFeng 说:
我的GCC可以编译啊,但是会产生一个指针类型不匹配的警告。
2010年6月 7日 09:58 | # | 引用
匿名懦夫 说:
没用??
这东西要是没用你手机上就不会有那么多软件可以用。
手机CPU没有浮点处理器,一切浮点运算皆是使用定点数实现。
将开发的算法移植到手机平台的过程中,会大量运用到本博文中提到的概念。
更进一步,大量电子产品中都没有浮点处理器,包括貌似很高级的导弹也是如此。
第一次海湾战争中,含冤死在飞毛腿导弹下的16名驻沙特美国大兵,会严重不同意你这个说法,正是因为爱国者导弹控制系统中定点数算法的累积误差,他们才会被没有被拦截到的飞毛腿导弹击中。
2010年6月 7日 21:03 | # | 引用
kain 说:
float* pFloat=#
这句一般是编译通不过的, 会报错, 我用VC试过了, 需要强制转换. 教材倒是都学过, 但是还真没注意到, 毕竟一般强制转换的都是类地址什么的, 基本数据类型间的转换倒是很少做.
2010年6月 7日 21:51 | # | 引用
Drosophila 说:
握爪~~我也在从头学C语言,而且也是看的这本书。挺好玩的。
楼上很多人说有没有用,我这非科班的业余人士不好做这种判断,不过我觉得,搞懂一个问题本身就是有趣且有意义的事清。
2010年6月 7日 23:59 | # | 引用
KingsamChen 说:
float* pFloat=# /* pFloat表示num的内存地址,但是设为浮点数 */
这句如果不用强制类型转换,编译器应该不让过吧~
2010年6月 8日 17:44 | # | 引用
LK 说:
很想知道浮点和定点的累积误差是怎么回事。。。
似乎浮点的误差是不可避免但可控,细节不清楚
请教
2010年6月13日 00:30 | # | 引用
Ruan YiFeng 说:
这是因为很多小数不能准确表示成二进制形式。比如0.4,你就无法写出它的精确二进制形式(即0.5的各次幂的累加),我们只能不断接近0.4,而不能达到它。
2010年6月13日 07:36 | # | 引用
墨叶 说:
事实上VC和BC内部存储也是不一样的,用过的应该有印象
2010年6月15日 15:18 | # | 引用
loveclan 说:
IEEE浮点数应该是不享受结合律和交换律的,所以使用时要特别小心。而且CPU浮点数寄存器精度和标准浮点数不一样,详见 http://book.douban.com/subject/1229948/《Computer Systems--A Programmer's Perspective》的第二章。
2010年6月26日 23:44 | # | 引用
嘟嘟 说:
等你做通信就知道多有用了,需要自己解析算的。
2010年7月22日 17:06 | # | 引用
pl 说:
说道浮点结构, 不得不提这个函数啊!!
float InvSqrt (float x)
{
float xhalf = 0.5f*x;
int i = *(int*)&x;
i = 0x5f3759df - (i>>1);
x = *(float*)&i;
x = x*(1.5f - xhalf*x*x);
return x;
}
传奇性的函数啊.
2010年8月28日 16:47 | # | 引用
matthew 说:
博文中的公式
V=(-1)^0×0.00000000000000000001001×2^(-126)=1.001×2^(-146)
里面的-146应该是-126吧(以为指数是1-127)
2010年9月16日 14:07 | # | 引用
mafai 说:
E的真实值必须再减去一个中间数,对于8位的E,这个中间数是127
比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
那么,第一位的符号位s=0,有效数字M等于001后面再加20个0,凑满23位,指数E等于3+127=130,即10000010。
上面是否应该是真实值加上一个中间数呢?因为下面两个例子均是使用 + 127
2010年9月20日 11:23 | # | 引用
timyuanzhiwei 说:
这个真的很有用! 废话不说,谢谢分享。。。。
2011年4月29日 22:41 | # | 引用
kevin 说:
(3)E全为1。这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);如果有效数字M不全为0,表示这个数不是一个数(NaN)。
请教,为什么这个case里面M要区别全为0和非全为0的情况?
2011年12月29日 21:50 | # | 引用
Robin 说:
不错。正好在看32位浮点数表示方法。原来有效位的第一位会省略的,主要是我看的计算机组成没讲清楚。现在豁然开朗。
2012年6月14日 09:16 | # | 引用
atupal 说:
可以转载嘛? 注明原文链接的
2012年8月22日 11:25 | # | 引用
OceanCloud 说:
然后,指数E还可以再分成三种情况:
(1)...
(2)...
(3)...
第2种情况中E是不是等于0-127(或者0-1023)?
2012年9月27日 00:10 | # | 引用
xudifsd 说:
博主关于第二部分中E=3+127解释得不多,详细见这篇文章的“规格化”部分
2012年10月29日 15:10 | # | 引用
river 说:
多谢博主的解答。发现你的博文配图很好,不知道你是用什么工具做的呢
2012年11月 1日 15:35 | # | 引用
robin 说:
不,应该就是-146,因为0.00000000000000000001001×2^(-126) = 0.00000000000000000001×1.001×2^(-126) = 1×2^(-20)×1.001×2^(-126) = 1.001×2^((-20)+(-126)) = 1.001×2^(-146)
2013年3月 2日 11:49 | # | 引用
hoot 说:
很受用
2013年5月 1日 20:15 | # | 引用
matrix3d 说:
斯坦福大学的编程范式公开课里就讲到了博主说说的这些
2013年5月 3日 09:34 | # | 引用
想听什么baby 说:
受用,谢谢。这些才是最本质的。
2013年5月16日 20:38 | # | 引用
小旺 说:
V=(-1)^0×0.00000000000000000001001×2^(-126)=1.001×2^(-146)
应该修改为:
V=(-1)^0×1.00000000000000000001001×2^(-126)
因为 M=000 0000 0000 0000 0000 1001(23b),转化为系数时,1自动加上,变成 1.000 0000 0000 0000 0000 1001(24b)
2013年9月 6日 23:35 | # | 引用
kaicui 说:
为什么指数要使用无符号整型来表示,然后在计算的时候再减去一个中间数?
为什么不直接使用有符号整数表示?
2013年11月 8日 12:07 | # | 引用
shmilyxbq 说:
做基础软件研发这些知识是绕不过去的,国内现在做的还少
2013年12月20日 17:14 | # | 引用
yiltoncent 说:
2014年1月25日 16:26 | # | 引用
yiltoncent 说:
错了 E为0,所以M不需要自动加一
2014年1月25日 16:27 | # | 引用
zeekvfu 说:
我是来吐槽博客页面排版的。:-)
关于代码的展示,个人觉得用 pre 标签比 blockquote 标签更合适。另外,对于每行代码都用 p 和 strong 标签,实现方式实在是有些 ugly。
另外没有代码高亮展示,不知道你中文博客用的什么框架(英文是 WordPress),可以找相关的代码高亮插件。
2014年4月14日 21:57 | # | 引用
koka 说:
E的真实值必须再减去一个中间数,对于8位的E,这个中间数是127
比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
那么,第一位的符号位s=0,有效数字M等于001后面再加20个0,凑满23位,指数E等于3+127=130,即10000010。
为什么是10+127而不是10-127呢?很多文章都描述规格化是E减去偏置值,但实现的时候却是加法。请指教!
2015年1月21日 20:04 | # | 引用
啊打发 说:
说明你没用到,不是没什么用
2015年2月28日 09:18 | # | 引用
0.618 说:
有一个更有趣的地方:如果将最后一句代码中的%f改为%d,即printf("*pFloat的值为:%d\n",*pFloat); 此时该值结果为0
2015年4月 6日 16:54 | # | 引用
yao 说:
请问博主画的图是用什么工具的?
2015年7月28日 16:59 | # | 引用
就是俺 说:
hehe, 那是因为你的水平 还用不到
2015年10月 3日 11:03 | # | 引用
还是俺 说:
"这样做的目的,是节省1位有效数字" 这个应该是“节省一位”吧,有效数字怎么能节省呢
2015年10月 3日 11:05 | # | 引用
genericyzh 说:
第三点直接跳到第四点了,没了4.
3. -> 5.
2016年1月19日 14:31 | # | 引用
puma 说:
因为E-127= 10, 所以E= 127 + 10 = 137。
2016年7月15日 11:27 | # | 引用
我不知道 说:
看来是因为翻译错误
2016年8月26日 00:04 | # | 引用
我不知道 说:
要用0到255表示负数,那么类似数轴,我们用127作为原点,大于127的是正数,小于127的是负数。
第0位是符号位,第1-8位如果计算机读出来是130,那么这表示E的实际值是130-127=3。
2016年8月26日 00:26 | # | 引用
kcats 说:
"然后,指数E还可以再分成三种情况:"的第1种情况表述有误, 应该是"E不全为0且不全为1"
2017年2月 8日 15:00 | # | 引用
CB 说:
例题的第二部分的解析是错误的,该浮点数的二进制形式的 exponent 部分 应该往右移一位
2017年3月 2日 20:43 | # | 引用
wub 说:
但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,E的真实值必须再减去一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。
比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
这个地方没有解释清楚,怎么上面说IEEE 规定,E的真实值必须再减去一个中间数,下面的比如又变成了10+127了?
我查了一下资料,只是这样理解了: 因为指数部分在存储时是在符号位之后,为了区分指数和符号位部分,因此在存储指数的时候会将指数部分向右偏移127(单精度), 结果将为0 ~ 254, 也就是存储时将E+127, 那获取值时才要减127,得到E的真实值。
2017年4月15日 13:56 | # | 引用
apolo 说:
讲的非常清楚,谢谢!
2017年7月 2日 16:09 | # | 引用
rolfzhang 说:
符号位0应该表示正数吧?
2017年9月16日 20:17 | # | 引用
SimonLiu 说:
@pl:
我就是看了这个函数,为了搞清楚怎么回事,才搜到博主这里来的。
2018年4月25日 17:56 | # | 引用
SimonLiu 说:
强制转换通过了,编译器是Apple LLVM version 9.1.0 (clang-902.0.39.1),不转换是通不过的。
2018年4月25日 17:59 | # | 引用
khejing 说:
文章中的公式其实是在已有二进制的情况下,如何得到其表示的浮点数。要想知道如何由一个浮点数得到其二进制表示,文中根本没有讲,就会导致整体还是不大理解。建议再补充看如下链接:https://ryanstutorials.net/binary-tutorial/binary-floating-point.php
2018年5月29日 19:22 | # | 引用
王调科 说:
阮一峰老师您好!
V=(-1)^0×0.00000000000000000001001×2^(-126)=1.001×2^(-146)
这个结果 1.1221598e-44 或者 2e-323。就算我用%.1000f来输出整数9,小数点后依然全是0。虽然理论上来说这个很小的数已经超出了浮点数的精度,但是如果是浮点数在那儿可以打印出小数点很多0后的小数位。、
我的疑问是:为什么是个整数却成了0.000000后面一亿位都是0。是因为整数转换后已经超出了浮点数的精度而且这个数十分接近0,%f得到的就是0了,所以%f输出的就是0.0。是这样理解吗?
2018年8月15日 22:13 | # | 引用
Kris 说:
@王调科:
我也做了同样的测试,在我的电脑上,就是把这一句改了:
printf("*pFloat的值为:%.50f\n",*pFloat); /* 显示num的浮点值 */
打印出来是:
*pFloat的值为:0.00000000000000000000000000000000000000000001261169
你要不再试试,换台电脑,重新gcc。
2018年9月29日 14:12 | # | 引用
cole_1996 说:
好巧我就在看斯坦福大学的编程范式第2集,其中有些细节部分不太懂来网上就看到这篇文章,查了下E部分全1在957标准中表示NaN族,是不是因此E的数字部分只能是非全0,全1外的,000...1 到 111...10这范围?
2018年10月21日 10:49 | # | 引用
robbin 说:
看了这么多文章 就这篇通俗易懂
2019年4月11日 11:31 | # | 引用
suyumo 说:
写的真的让人迷惑
二进制和十进制混着用
2019年5月27日 18:20 | # | 引用
周陆军 说:
https://www.zhoulujun.cn/html/theory/computBase/2016_0714_7860.html
引用了博主的内容
IEEE-745浮点数表示法数值精度丢失
计算机中的数字都是以二进制存储的,二进制浮点数表示法并不能精确的表示类似0.1这样 的简单的数字
如果要计算 0.1 + 0.2 的结果,计算机会先把 0.1 和 0.2 分别转化成二进制,然后相加,最后再把相加得到的结果转为十进制
但有一些浮点数在转化为二进制时,会出现无限循环 。比如, 十进制的 0.1 转化为二进制,会得到如下结果:
0.1 => 0.0001 1001 1001 1001…(无限循环)
0.2 => 0.0011 0011 0011 0011…(无限循环)
而存储结构中的尾数部分最多只能表示 53 位。为了能表示 0.1,只能模仿十进制进行四舍五入了,但二进制只有 0 和 1 , 于是变为 0 舍 1 入 。 因此,0.1 在计算机里的二进制表示形式如下:
0.1 => 0.0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 101
0.2 => 0.0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 001
用标准计数法表示如下:
0.1 => (−1)0 × 2^4 × (1.1001100110011001100110011001100110011001100110011010)2
0.2 => (−1)0 × 2^3 × (1.1001100110011001100110011001100110011001100110011010)2
在计算浮点数相加时,需要先进行 “对位”,将较小的指数化为较大的指数,并将小数部分相应右移:
最终,“0.1 + 0.2” 在计算机里的计算过程如下:
经过上面的计算过程,0.1 + 0.2 得到的结果也可以表示为:
(−1)0 × 2−2 × (1.0011001100110011001100110011001100110011001100110100)2=>.0.30000000000000004
这是一个典型的精度丢失案例,从上面的计算过程可以看出,0.1 和 0.2 在转换为二进制时就发生了一次精度丢失,而对于计算后的二进制又有一次精度丢失 。因此,得到的结果是不准确的。
2019年7月10日 21:23 | # | 引用
rangwer 说:
比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
这里没太明白..
2019年9月 3日 10:00 | # | 引用
Lee 说:
#include
#include
using namespace std;
int main(){
int d = 9;
float* pFloat = (float*)&d;
*pFloat = 9.0;
printf("%f %d\n",*pFloat,d);
printf("%d",9.0);
return 0;
} 为什么给地址后修改为浮点数可以正常输出,直接将浮点数用整型输出为就是0呢
2019年9月22日 20:55 | # | 引用
flamesnow 说:
1. 上文“(2)E全为0。这时,浮点数的指数E等于1-127(或者1-1023)”,这里为什么是1-127?而不是0 - 127呢??求解释
2. 上文最后面第二道题目“所以,写成二进制形式,应该是s+E+M,即0 10000010 001 0000 0000 0000 0000 0000。这个32位的二进制数,还原成十进制,正是1091567616。”,请问这里的“1091567616”是怎么算出来的?
在线等等?11点之前都在线,很想知道!!!!
2019年10月14日 21:51 | # | 引用
JASON 说:
E全为0。这时,浮点数的指数E等于1-127(或者1-1023)
这里应该是 0-127 或者 0-1023
2020年5月12日 15:37 | # | 引用
xxxx 说:
其实可以说和语言无关,是计算机内部存储方法,大部分语言都采用了相同的方式,是为了计算机指令执行更快更方便, 并不是每个语言 随便定义自己的实现方式
2021年1月 2日 21:44 | # | 引用
cctga 说:
double:-1.3
binary:-1.01,0011,0011,0011,... 无限循环 0011
科学计数法:-1.01,0011,0011... x 2^0
s = 1, E = 0 + 1023, M = 01,0011,0011,0011,0011... 循环到补足 52 位
所以结果为: 1 0111,1111,111 01,0011,0011,0011,0011,0011,0011,0011,0011,0011,0011,0011,0011,00
使用代码验证结果为: 1 0111,1111,111 01,0011,0011,0011,0011,0011,0011,0011,0011,0011,0011,0011,0011,01(发生进位)
2021年1月27日 22:58 | # | 引用
陈杰 说:
博主,请问一下,你举例中的5.0 转换成 1.01×2^2这部是如何计算出来的,如果5.2这样本身带有小数位的数,转换成s=0,M=1.01,E=2又该是如何咧?
2021年3月15日 11:07 | # | 引用
bonobo 说:
1.001×2^3这部分有误吧,应该是1.125×2^3, 1.001这里的001是二进制,0.1是十进制的0.5,0.001是0.125.
2021年4月26日 22:07 | # | 引用
W 说:
看评论区不少人在说自学非科班,我是个双非本科感觉平时基本靠自学了也是´•ﻌ•`,好的大学可能不是这个样
2021年12月24日 20:17 | # | 引用
bsc2xp 说:
@周陆军:
0舍1入的话,0.2 那个最后写错了吧,应该是 ....010
2023年8月11日 11:28 | # | 引用