上一次,我介绍了一些数论知识。
有了这些知识,我们就可以看懂RSA算法。这是目前地球上最重要的加密算法。

六、密钥生成的步骤
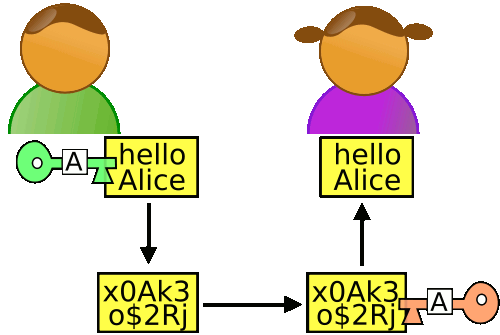
我们通过一个例子,来理解RSA算法。假设爱丽丝要与鲍勃进行加密通信,她该怎么生成公钥和私钥呢?
第一步,随机选择两个不相等的质数p和q。
爱丽丝选择了61和53。(实际应用中,这两个质数越大,就越难破解。)
第二步,计算p和q的乘积n。
爱丽丝就把61和53相乘。
n = 61×53 = 3233
n的长度就是密钥长度。3233写成二进制是110010100001,一共有12位,所以这个密钥就是12位。实际应用中,RSA密钥一般是1024位,重要场合则为2048位。
第三步,计算n的欧拉函数φ(n)。
根据公式:
φ(n) = (p-1)(q-1)
爱丽丝算出φ(3233)等于60×52,即3120。
第四步,随机选择一个整数e,条件是1< e < φ(n),且e与φ(n) 互质。
爱丽丝就在1到3120之间,随机选择了17。(实际应用中,常常选择65537。)
第五步,计算e对于φ(n)的模反元素d。
所谓"模反元素"就是指有一个整数d,可以使得ed被φ(n)除的余数为1。
ed ≡ 1 (mod φ(n))
这个式子等价于
ed - 1 = kφ(n)
于是,找到模反元素d,实质上就是对下面这个二元一次方程求解。
ex + φ(n)y = 1
已知 e=17, φ(n)=3120,
17x + 3120y = 1
这个方程可以用"扩展欧几里得算法"求解,此处省略具体过程。总之,爱丽丝算出一组整数解为 (x,y)=(2753,-15),即 d=2753。
至此所有计算完成。
第六步,将n和e封装成公钥,n和d封装成私钥。
在爱丽丝的例子中,n=3233,e=17,d=2753,所以公钥就是 (3233,17),私钥就是(3233, 2753)。
实际应用中,公钥和私钥的数据都采用ASN.1格式表达(实例)。
七、RSA算法的可靠性
回顾上面的密钥生成步骤,一共出现六个数字:
p
q
n
φ(n)
e
d
这六个数字之中,公钥用到了两个(n和e),其余四个数字都是不公开的。其中最关键的是d,因为n和d组成了私钥,一旦d泄漏,就等于私钥泄漏。
那么,有无可能在已知n和e的情况下,推导出d?
(1)ed≡1 (mod φ(n))。只有知道e和φ(n),才能算出d。
(2)φ(n)=(p-1)(q-1)。只有知道p和q,才能算出φ(n)。
(3)n=pq。只有将n因数分解,才能算出p和q。
结论:如果n可以被因数分解,d就可以算出,也就意味着私钥被破解。
可是,大整数的因数分解,是一件非常困难的事情。目前,除了暴力破解,还没有发现别的有效方法。维基百科这样写道:
"对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之,对一极大整数做因数分解愈困难,RSA算法愈可靠。
假如有人找到一种快速因数分解的算法,那么RSA的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA密钥才可能被暴力破解。到2008年为止,世界上还没有任何可靠的攻击RSA算法的方式。
只要密钥长度足够长,用RSA加密的信息实际上是不能被解破的。"
举例来说,你可以对3233进行因数分解(61×53),但是你没法对下面这个整数进行因数分解。
12301866845301177551304949
58384962720772853569595334
79219732245215172640050726
36575187452021997864693899
56474942774063845925192557
32630345373154826850791702
61221429134616704292143116
02221240479274737794080665
351419597459856902143413
它等于这样两个质数的乘积:
33478071698956898786044169
84821269081770479498371376
85689124313889828837938780
02287614711652531743087737
814467999489
×
36746043666799590428244633
79962795263227915816434308
76426760322838157396665112
79233373417143396810270092
798736308917
事实上,这大概是人类已经分解的最大整数(232个十进制位,768个二进制位)。比它更大的因数分解,还没有被报道过,因此目前被破解的最长RSA密钥就是768位。
八、加密和解密
有了公钥和密钥,就能进行加密和解密了。
(1)加密要用公钥 (n,e)
假设鲍勃要向爱丽丝发送加密信息m,他就要用爱丽丝的公钥 (n,e) 对m进行加密。这里需要注意,m必须是整数(字符串可以取ascii值或unicode值),且m必须小于n。
所谓"加密",就是算出下式的c:
me ≡ c (mod n)
爱丽丝的公钥是 (3233, 17),鲍勃的m假设是65,那么可以算出下面的等式:
6517 ≡ 2790 (mod 3233)
于是,c等于2790,鲍勃就把2790发给了爱丽丝。
(2)解密要用私钥(n,d)
爱丽丝拿到鲍勃发来的2790以后,就用自己的私钥(3233, 2753) 进行解密。可以证明,下面的等式一定成立:
cd ≡ m (mod n)
也就是说,c的d次方除以n的余数为m。现在,c等于2790,私钥是(3233, 2753),那么,爱丽丝算出
27902753 ≡ 65 (mod 3233)
因此,爱丽丝知道了鲍勃加密前的原文就是65。
至此,"加密--解密"的整个过程全部完成。
我们可以看到,如果不知道d,就没有办法从c求出m。而前面已经说过,要知道d就必须分解n,这是极难做到的,所以RSA算法保证了通信安全。
你可能会问,公钥(n,e) 只能加密小于n的整数m,那么如果要加密大于n的整数,该怎么办?有两种解决方法:一种是把长信息分割成若干段短消息,每段分别加密;另一种是先选择一种"对称性加密算法"(比如DES),用这种算法的密钥加密信息,再用RSA公钥加密DES密钥。
九、私钥解密的证明
最后,我们来证明,为什么用私钥解密,一定可以正确地得到m。也就是证明下面这个式子:
cd ≡ m (mod n)
因为,根据加密规则
me ≡ c (mod n)
于是,c可以写成下面的形式:
c = me - kn
将c代入要我们要证明的那个解密规则:
(me - kn)d ≡ m (mod n)
它等同于求证
med ≡ m (mod n)
由于
ed ≡ 1 (mod φ(n))
所以
ed = hφ(n)+1
将ed代入:
mhφ(n)+1 ≡ m (mod n)
接下来,分成两种情况证明上面这个式子。
(1)m与n互质。
根据欧拉定理,此时
mφ(n) ≡ 1 (mod n)
得到
(mφ(n))h × m ≡ m (mod n)
原式得到证明。
(2)m与n不是互质关系。
此时,由于n等于质数p和q的乘积,所以m必然等于kp或kq。
以 m = kp为例,考虑到这时k与q必然互质,则根据欧拉定理,下面的式子成立:
(kp)q-1 ≡ 1 (mod q)
进一步得到
[(kp)q-1]h(p-1) × kp ≡ kp (mod q)
即
(kp)ed ≡ kp (mod q)
将它改写成下面的等式
(kp)ed = tq + kp
这时t必然能被p整除,即 t=t'p
(kp)ed = t'pq + kp
因为 m=kp,n=pq,所以
med ≡ m (mod n)
原式得到证明。
(完)


杨琪 说:
数学乃万物之源呐
2013年7月 4日 12:47 | # | 引用
会林 说:
第一时间过来感谢阮先生无私奉献如此易懂的算法原理!
2013年7月 4日 12:52 | # | 引用
我叫小井 说:
终于体会到什么叫“深入浅出”
2013年7月 4日 12:53 | # | 引用
Black 说:
受益匪浅,谢谢!
2013年7月 4日 14:10 | # | 引用
joymufeng 说:
又一篇好文,感谢阮兄的无私分享!
2013年7月 4日 15:47 | # | 引用
Du 说:
如果量子计算机实现的话是不是就能破解了?
2013年7月 4日 17:33 | # | 引用
Ray 说:
RSA的困难性是基于大整数因子分解在计算上不可行,如果计算能力上去的话,当然是可以破解现有的密码。
2013年7月 5日 02:38 | # | 引用
RayJoy 说:
数学自有其独特的魅力。
2013年7月 5日 08:46 | # | 引用
t.k. 说:
九的子标题(2)m与n不是互质关系中
应该是“m与q必然互质”。
另外,数学公式用mathjax会更好看一些。
2013年7月 5日 16:56 | # | 引用
asdf 说:
[(kp)q-1]h(p-1) × kp ≡ kp (mod q)
可以直接一步得到结论了,何必之后那几步推导?
2013年7月 5日 18:48 | # | 引用
iljyya 说:
没看懂好伤心。
2013年7月 7日 08:33 | # | 引用
zhangyuqin 说:
不太明白,继续琢磨一下!
2013年7月 8日 10:34 | # | 引用
zz 说:
第四步计算模反元素下面这俩式子貌似符号弄错了~
ex + φ(n)y = 1
已知 e=17, φ(n)=3120,
17x + 3120y = 1
2013年7月 9日 00:06 | # | 引用
软件局局长 说:
当年数学没学好,看得快哭了。
2013年7月17日 09:42 | # | 引用
邹邹 说:
只看懂了个大概,不过对RSA算法有一个很好的印象了。这真是一篇好文章呀,阮兄的文章没有白付费呀。
2013年8月10日 16:56 | # | 引用
felix021 说:
别说DES……这个加密算法因为太容易被破解早就被废除了,建议改成3DES或AES.
2013年8月14日 10:57 | # | 引用
waveacme 说:
精彩啊,这两篇文章
2013年8月14日 13:16 | # | 引用
wusuopubupt 说:
精彩!!!
2013年8月16日 12:02 | # | 引用
STL 说:
谢谢你的文章。想问个问题,那个鲍勃向爱丽丝发消息的例子是单向的,如果爱丽丝想回复的话该怎么办呢?这时候是不是必须先协商一个密钥然后对称加密?
2013年9月10日 12:15 | # | 引用
nkAmerica 说:
为了让mod作用于n,而不是q。
2013年9月10日 17:17 | # | 引用
nkAmerica 说:
根本没有协商过程啊。都是用对方的公钥加密
2013年9月10日 17:19 | # | 引用
Lynx 说:
谢谢博主的文章。
请问一下,
m^e ≡ c (mod n)这公式怎么来的?
只是e跟φ(n)互质啊
2013年9月24日 15:42 | # | 引用
李华 说:
想到这个算发的人太伟大了,这是一个回答纯数学有什么用的最好案例。还有没有其他的像RSA这样简单有效的非对称加密方法呢?恐怕像找外星人一样难了。
2013年10月 9日 14:16 | # | 引用
frank 说:
DES废除的原因一个是密钥位数太少,在现在的计算能力下,已经无法保证安全,第二个原因是,DES是为硬件加密设计的,对于现在软件来说计算效率不够好,第三个原因是,一直有人怀疑DES的S盒中隐藏着后门,而这个后门被美国安全局掌握。所以提出了AES
3DES理论密钥长度为56*3=168bits,但是,在受到中间人攻击的条件下,退化为112bits。其安全性仍然不够好
2013年10月15日 22:52 | # | 引用
Martin.Hsuching 说:
写的很不错,浅显易懂,但看完,觉得最后一段有个疑惑,请教一下:(kp)ed = tq + kp
这时t必然能被p整除,即 t=t'p,这个必然性是如何证明的?请指导下~~谢谢
2013年10月28日 21:44 | # | 引用
LCS 说:
为什么公匙不能猜测的进行解密呢。。。
2013年11月 2日 23:14 | # | 引用
锦衣卫加密顾问 说:
正在做加密产品,以应对来自霉国的窃听威胁,感谢楼主的理论分析。
2013年11月 3日 03:51 | # | 引用
Chil 说:
这两篇文章写的太好了,对RSA算法浅入深出,让我明白很多。但有一个地方没看明白:博主写道
加密就是算出 me ≡ c (mod n)中的c
我想问一下,为什么要这样做?和上篇文章中什么地方有联系?还是就是这么规定的?
2013年11月11日 07:27 | # | 引用
哇哈哈 说:
此时,由于n等于质数p和q的乘积,所以m必然等于kp或kq
這個怎麼得來的?
m不是明文嗎,明文爲什麽一定等於kp或者kq?
2013年11月11日 16:35 | # | 引用
guanwh 说:
想双向通信的话肯定要定义两套公钥和秘钥了,都用对方的公钥加密发送,然后接收方用自己的秘钥解密就OK了!
2013年11月19日 20:29 | # | 引用
明天有风吹 说:
终于明白rsa是怎么一回事了,thanks!!
2013年11月26日 16:15 | # | 引用
L 说:
量子计算机是并行的,1024位的密码用1024个量子处理单元做计算,只要1秒。只是现在技术最多能做到8位量子处理单元的级别。so...
2013年12月12日 19:54 | # | 引用
Leon 说:
两边同时整除p,又p、q互质,于是t必定是p的整数倍。
2013年12月30日 21:08 | # | 引用
Leon 说:
数学角度:m、n不是互质关系,说明m、n必定含有非1公因子,而n等于质数p和q的乘积,因此m必然等于kp或kq。
2013年12月30日 21:16 | # | 引用
Gavin 说:
一直在使用RSA,但是不是很清楚RSA的数学原理,今天一看,胜读几年书!!!
1、to 哇哈哈:
此时,由于n等于质数p和q的乘积,所以m必然等于kp或kq
因为m与n不是互质关系,说明m与n有共同的公因子g,假设m=hg,由于n=pq,p与q互质,n只有p和q两个因子,所以g和h必然有一个等于q或者p, 所以才有结论“m必然等于kp或kq”
2、to Martin.Hsuching :
因为(kp)ed = tq + kp,=>(p)ed*(k)ed = tq + kp,=>
(p)ed*(k)ed - kp = tq,=>
p[(p)(ed-1)*(k)ed - k ] = tq,
左边是p的倍数,那右边必然也是p的倍数。因为p与q互质,所以t必然是p倍数,即 t=t'p
3、
2013年12月31日 16:43 | # | 引用
赵三 说:
2014年1月 2日 15:19 | # | 引用
赵三 说:
帮我理解了不少,感谢!还有一点向您请教下:
1.“(1)m与n互质。
根据欧拉定理,此时mφ(n) ≡ 1 (mod n)
得到(mφ(n))h × m ≡ m (mod n)”这个是怎么得到啊?(mφ(n))h≡1(mod n)这样写,对吗?接着,后面又多乘以个m,就能变成这样啦(mφ(n))h × m ≡ m (mod n),这个是为什么呢?
2.这个跟1.应该是同样的问题“(kp)q-1 ≡ 1 (mod q)
进一步得到[(kp)q-1]h(p-1) × kp ≡ kp (mod q)”这个也是,左右都乘以kp,这是为什么呢?
3.这个是我看RSA算法原理(一)中的疑问:“因此,7的任意次方的个位数(例如7的222次方),心算就可以算出来”这是怎么得到的呢?我只想到了:7的222次方=7的2次方*7的(4*55)次方,下面就不知道了。还望解惑,不胜感激~
2014年1月 2日 17:52 | # | 引用
dongxf 说:
如果量子计算机可以破解1024bit的RSA,那么可以用量子计算机做更长bit位的加密,比如2048bit...,直到无法破解
2014年1月 5日 17:07 | # | 引用
none 说:
to:赵三
1,(mφ(n))h≡1(mod n)这样写是对的,这个可以通过≡的含义,然后通过一个推导(也就是从h-1到h的推导)可以看出是正确的。比如设(mφ(n))h=r1*n+1,然后(mφ(n))h*m=(r1*n+1)*m,这个和n的余数就是m。
2,RSA算法原理(1)中回复里面有这个问题。7的(4*55)的余数就是1,然后7的2次方的余数为9,那结果就是9
2014年1月 7日 21:26 | # | 引用
colde 说:
证明
(m^e - kn)^d ≡ m (mod n)
等同于证明
m^ed ≡ m (mod n)
卡住在这里了,麻烦帮忙解释一下。
2014年1月12日 10:40 | # | 引用
八戒 说:
相当详实生动,非常感谢,,,,就是举例子的数字有点大了,,普通计算机直接正无穷大了,,,
2014年1月12日 22:59 | # | 引用
ssapym 说:
问个问题,
1,这个巨大的质数或那两个相乘质数从哪来的,2048位的从哪来的。RSA算法的可靠性依赖于大整数的因数分解,是一件非常困难的事情,那大整数现在最大到多少了,2048位以上的现在有么,好像还有什么美国输出限制。
2,如果分解困难,用现在产生大质数的算法,是否可以反推出来大质数,产生一个对应列表,就像md5的彩虹表,是否就可以破解。
谢谢
2014年1月13日 15:32 | # | 引用
王为雄 说:
你好,我觉得第五步骤里面:
所谓"模反元素"就是指有一个整数d,可以使得ed被φ(n)除的余数为1。
这句话后半句,应该是使得 φ(n) 被ed除的余数为1。
这是来自wiki的除法举例:
15 可以被 5 整除,记作 5|15。
文章中本意应该是ed除以φ(n)的余数是1的逻辑。
2014年1月14日 10:37 | # | 引用
luke 说:
其它都很清晰,第5步跳的太快了:
ed ≡ 1 (mod φ(n))
怎么就得到
ed - 1 = kφ(n)? K从哪里来?是不是从第一篇中这里来(b+kn 都是a的模反元素)?
再变成
ex + φ(n)y = 1,这时候K是不是就是Y了?X就是D了?
2014年1月19日 22:57 | # | 引用
luke 说:
问了一下同事,明白了!!! ed ≡ 1 (mod φ(n)) 意味着,ed除以φ(n)余1,于是,ed-1就能被φ(n)整除。能被整除就意味着 ed-1=kφ(n),k是任意一个整数。
2014年1月20日 17:53 | # | 引用
luke 说:
唉,我也卡在这里了。求高人继续。
2014年1月21日 15:48 | # | 引用
luke 说:
而 (m^e - kn)^d ≡ m (mod n)
意味着,(m^e-kn)^d - m = kn
所以,m^(ed)-kn - m = kn
得到,m^(ed) - m = 2kn => m^(ed) - m = kn (这里k只是代表一个整数倍的关系,值并不重要)
而 m^(ed) - m = kn 正意味着 m^(ed) ≡ m (mod n)
2014年1月21日 17:23 | # | 引用
mine260309 说:
2^1024大约是10^308这个数量级,包含的素数可以由素数定理知道大约是x/ln(x)这个数量级,可选的素数p和q太多了,p*q的组合就更多了,怎么做彩虹表?
彩虹表是基于有一些常用的密码(比如password, 123456)算出来的,你随机选一个密码,多半不会出现在彩虹表中。同理,你随机选两个p,q,怎么查彩虹表?
2014年1月24日 11:23 | # | 引用
鹿 说:
找到高人了,写得清楚,有例子,每步都写出原理。
2014年2月14日 22:00 | # | 引用
gk 说:
谢谢阮老师深入浅出的讲解,我知道了RSA算法是怎么回事儿了。
我感觉那些严谨的证明过程不必细致追究,主要是搞清楚RSA算法是什么,除非那些数学专业的。
2014年2月18日 21:47 | # | 引用
介木 说:
我无法读懂上面的数学公式.
请问,高中水平的我,需要学习那些书本,才能看懂上面的公式呢?
谢谢各位.
我懂质数
2014年2月24日 14:57 | # | 引用
David 说:
高中确实不涉及这方面的知识。找点关于余数的数论书看,知道基本的同余定理就行了。
2014年2月24日 20:38 | # | 引用
llxxtnt 说:
我有个问题
根据 c^d ≡ m (mod n)
加密者不知道私钥d,但是他知道明文m,密文c,以及n,是否可以推算出私钥d
2014年3月 4日 13:57 | # | 引用
llxxtnt 说:
还有一个问题,我是做金融的,在金融领域经常用到转加密这个概念
1. 老张先用公钥e1对明文m加密得到密文c1,然后将密文c1传递给老王
2. 老王收到密文c1后,用公钥e2替换公钥e1,得到密文c2
我想知道公钥e2替换公钥e1的具体过程
是先用私钥d1解密密文c1,还原出明文m以后,再用公钥e2对明文m加密得到密文c2
还是在一个原子过程中,直接就可以用私钥d1,公钥e2,密文c1计算出新密文c2,在计算过程中可以避免出现明文m?
2014年3月 4日 14:38 | # | 引用
袁定平 说:
您好,以前看过你的这篇文章了,最近在看一个系统teamcity的登录过程,它会先给用户发一个公钥,然后用这个公钥对密码进行加密,发给服务器,从我看来,好像每次它发过来的公钥都是同一个串,是不是说只要有足够的计算力和足够的时间,我从这个公钥推出了其中的私钥,就可以破解用户发给它的所有密码?
我比较困惑的是,如果一个系统的安全系数要求很高的话,不需要经常更换公钥吗?
有没有可能一个经常破解密码的人,在一个地方看到一个公钥正好是他之前破解过的,那他也就能轻易破解新系统的密码? 我们所能使用的公钥理论上市无限的吗?
希望能够解答,谢谢
2014年3月 7日 16:54 | # | 引用
tommyqian_2008 说:
第四步,随机选择一个整数e,条件是1
e不一定要小于φ(n)吧,根据欧拉定律,e只要跟φ(n) 互质就可以了
求大神解惑
2014年5月 9日 11:09 | # | 引用
hai 说:
个人观点:
1,公钥本来就是公开的,没有必要更换;
2,公钥不可能(所需时间和计算力无比的巨大)推算出私钥;
3,首先一个人不可能破解过一个公钥。其次是简单的算法,私钥对应一个确定的公钥,这是有风险的,所以现在的加密算法还使用了随机数,破解不可能,运气更不可能。
2014年6月 5日 17:46 | # | 引用
啊啊 说:
每个个体都有自己的公钥和私钥,在通信中,故爱丽丝也有自己的公钥和私钥。
2014年6月 8日 16:18 | # | 引用
jimohou 说:
(kp)^ed = tq + kp => tq = (kp)(kp^ed-1 - 1)
因为p,q是互质,所以kp必然不能整除q,那么就必然整除t,t=t'p
2014年6月26日 15:32 | # | 引用
[email protected] 说:
我的看法:
p*q的积的二进制的位数如果固定并确定为1024,则p和q的取值只能在一定范围内取,这在RSA密钥生成软件中自然会有指定。如果所有的密钥生成机制都按同一规定,那么由于素数资源不是随机无限的(有素数生成机制的限制,有随意取两个素数的乘积的二进制位数的限制),设素数资源的个数为n,在有限的素数资源中取出两个数的可能组合将是C|(2,n)。将每个组合的乘积一一列出,就可以组成彩虹表,可以从乘积列表中查找出对应的素数组合,进而推出公钥和私钥。素数资源不够的软件产生的密钥,尤其具有这样的隐患,看似很安全,实际上人家大的机构很容易破解出私钥来。所以,生产大素数的机构就像开矿公司,也像数字银行,拥有的素数资源越多越安全。不知是否可以这样理解?
不同机构产生的证书(包括私钥、公钥)的质量(指安全保证)是良莠不齐的。
我想ssapym彩虹表的本意即在如此。
2014年7月21日 12:40 | # | 引用
alphaqcode 说:
(m^e - kn)^d ≡ m (mod n)
分解下左边公式
(m^e - kn)^d = m^ed + [(m^e)^d-1]*kn + [(m^e)^d-2]*kn^2 + ....
除了第一个m^ed,后面的数都含有XXX*kn,所以都能被n整除
2014年7月22日 16:23 | # | 引用
xidactw 说:
受益匪浅
2014年7月24日 11:28 | # | 引用
lbs 说:
大哥,那个模反元素有问题
一说:
a* a的[φ(n)-1] % n = 1
二说:
a* a的[φ(n)-1] % φ(n) = 1
明显不一样了丫、。。。。
2014年7月24日 21:41 | # | 引用
shindo 说:
这步mφ(n) ≡ 1 (mod n)
到
(mφ(n))h × m ≡ m (mod n)
实在看不懂,能否详细解释下?
2014年7月31日 10:09 | # | 引用
shindo 说:
我懂了, mφ(n) ≡ 1 (mod n) => mφ(n) = K n +1 , k为自然数
(kn + 1)^h 展开多项式,除了1以外,全部含有kn, 所以其他项都能被n整除而余1..
也就是能推出 (mφ(n))h ≡ 1 (mod n)
然后m 这个中间数学gap还是挺大的...
2014年7月31日 14:26 | # | 引用
nan 说:
调理清晰,把一个复杂难懂的数学问题,一步一步分解,深入浅出,容易理解,学习了!
2014年8月23日 19:07 | # | 引用
Jayce 说:
文章超赞……
要是你能加上怎么快速生成的方法,相信对读者更有帮助,因为我找到这篇文章是因为我想快速生成公钥私钥来用,而我又是刚接触linux:
ssh-keygen -t rsa
2014年9月 4日 10:42 | # | 引用
ax_pokl 说:
RSA加密解密算法中,已知公钥和密匙n,e,d,是否能将合数n=p*q分解?
先温故一下RSA算法:
1、两个大质数p,q。
2、模数n=p*q。
3、欧拉函数f=(p-1)(q-1)。
4、随机数e,1 5、模逆d,即最小整数d,e*d=1 mod f。
也就是说:
知道了p,q也就知道了n,f;
知道了f,e也就知道了d。
下面温故一下加密解密算法:
已知明文m,满足m 加密:密文c=m^e mod n。
解密:明文x=c^d mod n。
证明一下解密得到的明文x=m:
由c=m^e mod n,得c=m^e+k*n。
代入x=c^d mod n,得x=(m^e+k*n)^d mod n。
于是x=m^e^d mod n,即x=m^(e*d) mod n。
由于e^d=1 mod f,得e*d=k*f+1。
代入得x=m^(kf+1) mod n,x=m*m^(kf) mod n。
当m与n互质时,x=m*(m^f)^k mod n,由欧拉定理可知x=m mod n。
又m 当m与n不互质时,由于n=p*q且m 若m=kp,则m^(q-1)=(k*p)^(q-1)=1 mod q。
接着[(k*p)^(q-1)]^[k*(p-1)]*kp=kp mod q,即(k*p)^(e*d)=k*p mod q。
又由于(k*p)^(ed)=k*q+k*p,(k*p)^(ed)=k*q*p+k*p,。
所以m^(ed)=m mod n,x=m。
即证。
2014年9月 9日 22:05 | # | 引用
ax_pokl 说:
现在考虑以下问题:
已知n和d,是否能将n分解?
可将这个问题分为几个问题:
1、已知n和f,是否能将n分解?
2、已知n,e和d,是否能得到f?
3、已知n和d,是否能得到e?
4、已知d和f,是否能得到e?
对于问题1的回答是肯定的。
n-f+1=sum=p+q,用二分法厉遍p,得p(sum-p)和n比较大小,即可快速确定p,q的值。
所以知道了n,f,就知道了p和q。也就是说,p,q,n,f四个数知道任意两个就可以知道全部。
那么,问题2就来了。如果p,q,n,f只知其一,又知道了e和d,是否能知道其它三个数呢?
最常见的情况就是知道了n,e和d。
由e*d=1 mod f,知e*d=k*f+1。
根据的同余方程定理可以知道存在k 并且d,k始终互质,由e,f互质又可推出e,k互质和f,d互质。
现在的问题又变为,e,d,f三个数各知道两个,能否知道第三个数?在已知n的情况下又是如何呢?
已知e,f可知道d,已知e,d不可知道f。
已知d,f,因为d,f互质,所以模逆e必存在,e必然在f的同余类中。又e 也就是说,e,f求d和d,f求e的过程是相同的。
这样,问题4的回答就是肯定的。
我们还可以发现,问题3的回答是否定的。
e和d对于f的地位是等价的,我们显然不可能用公匙n,e得到密匙n,d,所以反之亦然。
于是我们发现,f是十分重要的。知道了f,那么e和d就能互求。知道了f,那么n,p,q就能互求。
最后我们回到问题2。由于n,p,q的地位是等价的,我们可以换个死路考虑。
在已知p,e,d的情况下能否知道f和n?由e*d=k*f+1可以算出k*f。
然后又知道了p,可以算出k*(p-1)(q-1)/(p-1)=k*(q-1)。
然而这样组合的数量是很多的,如果不知打k,我们不可能知道q。所以知道p,e,d不能知道f或n。
那么知道n,e,d,也就是知道n和k*f,也就是知道p*q和k(p-1)(q-1)的情况下呢?
由于k是不可知的,k值的不同会导致f产生很大的变化。
我们虽然知道上限n,但直接拿f去除以n显然不能得到正确的k。
由于p和q的差值可能很大也可能很小,所以除出来的结果可能十分接近k也可能和k差很多。
于是无法缩小搜索p和q的范围,也无从使用二分法。
所以我认为,已知n,e,d是无法得到f的,同样也无法得到p和q。
如果大家有办法分解n的话,求详细的算法。
2014年9月 9日 22:05 | # | 引用
陈佳 说:
正在查rsa的资料,又回到了这里,想自己实现一个简易的rsa。
2014年9月 9日 22:50 | # | 引用
卢磊 说:
这种解释说法就是“鸡生蛋,蛋生鸡”问题,拿着要证明的结果作为证明的已知条件来证明问题!!!
2014年9月13日 23:15 | # | 引用
link 说:
第一次看懂了rsa算法, 真是好文章
2014年9月13日 23:24 | # | 引用
卢磊 说:
对头,到这就可以截止了,况且后面证明的很乱
2014年9月14日 00:28 | # | 引用
电小弟 说:
好像和CLRS算法差不多,但是各有各的特点及其长处.
2014年9月14日 03:09 | # | 引用
ax_pokl 说:
突然发现,双方的公钥和私钥对换,还是能够顺利加密和解密的。
2014年9月19日 07:49 | # | 引用
NeroLee 说:
以 m = kp为例,考虑到这时k与q必然互质。
这句话不对吧,比如说m=3n=3qp不行吗,那么k=3q,哪来必然互质?应该再细分
2014年9月30日 16:52 | # | 引用
zoudaokou2006 说:
根据RSA规范,要加密的信息m,范围为0~n-1,所以你说的不成立。
5.1.1 RSAEP
RSAEP ((n, e), m)
Input: (n, e) RSA public key
m message representative, an integer between 0 and n– 1
Output: c ciphertext representative, an integer between 0 and n– 1
2014年10月23日 11:42 | # | 引用
NeroLee 说:
Thanks. 现在懂了。
2014年10月27日 14:49 | # | 引用
番石榴 说:
我看到了未来的密钥是1mb起码。。。。。。
2014年11月11日 09:48 | # | 引用
王军 说:
65^17 ≡ c (mod 3233)
说等于
65^17 ≡ 2790 (mod 3233)
即c等于2790
想请问下,这里的2790是怎么算出来的??
2014年11月26日 14:46 | # | 引用
Lin 说:
“m与q必然互质”没错,因为m=kq
2014年11月26日 14:49 | # | 引用
王军 说:
65^17 ≡ c (mod 3233)
说等于
65^17 ≡ 2790 (mod 3233)
即c等于2790
想请问下,这里的2790是怎么算出来的??
我指的是口算或者笔算 不是利用计算机算65的17次方除以3233
有没有简单算法 如果笔算65的17次方 会死人的。。。
2014年11月26日 15:59 | # | 引用
Jecvay 说:
一口气看完两篇, 果然精彩
2014年11月30日 02:07 | # | 引用
wfade 说:
k与q必然互质
卡在这里了
2014年12月18日 16:36 | # | 引用
君升 说:
你好,请教一下:像12306这样的网站,在使用时要下载他的证书并导入,这时下载的证书是证书请求文件CSR吗?还是已经经过签名的公钥了?
2014年12月22日 12:49 | # | 引用
kellen_yan2014 说:
终于搞懂了,非常感谢!
2014年12月26日 10:54 | # | 引用
漠上花开 说:
刚接触RSA时看过其他网上的微博,要么是粘贴过来的,要么是片面不详细。今天看了阮先生描写的原理,顿时醍醐灌顶,把我所有没有搞懂的、有疑问的统统说清楚了,特别是数论原理,推导的过程描述的很详细。还结合实际中的密钥的长度、实际当中的数值,这些是刚接触加密算法的时候都有的疑问,这两篇文章都描写的非常详细,真的受益匪浅,而且特别欣赏这种写作风格,严谨、有据。真的谢谢
2015年1月 8日 10:45 | # | 引用
tim 说:
博主写的文章让人涨知识!
2015年1月14日 21:38 | # | 引用
tomas 说:
这是我见过的最通俗易懂的解释!!
2015年1月27日 19:52 | # | 引用
Jack 说:
谢谢lz。
但有个问题,“如果私钥被攻破,那么消息就会被破解”。这里是不是隐含了解密算法或者是加密算法,可以认为是公开的了,至少是容易获得的。
如果是这样,为什么不能从加密算法和已知的公钥已经加密后的信息,反推出原始信息呢?
2015年2月 3日 14:42 | # | 引用
傅琦佳 说:
您好,我看了网易公开课中的现代密码学,再看了您的文章感觉清晰很多,但有一点一直不大懂,求d时用到“拓展欧几里得算法”具体应该怎么算?
我对这方面很有兴趣,高中数学竞赛也学过一些数论知识(现在大一),但受专业限制接触不到这方面知识,打算通过网易公开课自学,纯粹出于兴趣。希望有机会与您多交流学习。
2015年2月27日 15:29 | # | 引用
小史 说:
百度百科里关于扩展欧几里得算法有讲具体怎么做。
2015年3月11日 15:17 | # | 引用
陈睿 说:
豁然开朗,十分感谢
2015年4月16日 15:47 | # | 引用
袁宇阳 说:
有一个疑问,就是在加密的时候 用的这个式子:m的e次方 ≡ c (mod n) 来计算出的c ,然后之后是把c给了爱丽丝让爱丽丝拿私钥去解m,我想问的是这时候知道c,可不可以还用之前那个得出c的式子: m的e次方 ≡ c (mod n) 再反过去解出m,因为这时候n,c,e都已知。m就等于 c (mod n)再开e次方了。 大神快粗来,急,在线等~~
2015年4月25日 14:42 | # | 引用
杨国宝 说:
第二次看了,还是没看太懂。下次继续学习。谢谢阮老师
2015年4月29日 17:13 | # | 引用
Caleb 说:
65^17 ≡ 2790 (mod 3233) 这个式子成立吗?
2790 mod 3233 = 2790
65^17 mod 3233 = 887 (matlab得到的结果)
另外 2790^2753 ≡ 65 (mod 3233) 这个式子中的 2790^2753 这个值,计算机可以算出来吗?
谢谢
2015年5月29日 18:11 | # | 引用
Codisan 说:
还是有个疑问:
alice 回信的时候,咋整?
bob发信: bob(公钥加密) -> alice (私钥解密),这个逻辑我明白
alice 回信, 这个怎么处理?求解!!
2015年6月12日 20:54 | # | 引用
我大哥海鹏 说:
把(m^e - kn)^d 完全展开后只有一项不包含n的项 m^ed m^ed对n取余就等于 (m^e - kn)^d 对n取余
2015年6月15日 18:49 | # | 引用
我谁也不是 说:
bob给alice发信,用的是Alice的公钥,Alice用自己的私钥解密;如果Alice要给bob回信,就换成bob的公钥加密,bob用自己的私钥解密。
2015年6月18日 13:16 | # | 引用
骆驼 说:
怒赞!!!!
2015年7月10日 11:32 | # | 引用
ax_pokl 说:
模幂法:
依次计算65^2 mod 3233, 65^4 mod 3233, 65^8 mod 3233, 65^16 mod 3233,最后再将65^16 mod 3233的结果和65相乘再mod 3233,这样可以保证最多只要做2*log3(n)次大数乘法和大数取模运算就可以得出结果了。
2015年7月13日 19:50 | # | 引用
悟空 说:
感谢博主,虽然对数学的还没有完全搞懂,但是基本上能浅显理解RSA的理论基础了,感谢感谢。
2015年7月17日 16:24 | # | 引用
lingjie_ding 说:
阮先生好,我在看的时候也会有@袁宇阳 的问题,可以直接拿公钥和加密后的数据反推出加密之前的数据吗?
2015年8月16日 17:48 | # | 引用
scateu 说:
"以 m = kp为例,考虑到这时k与q必然互质,则根据欧拉定理,下面的式子成立:"
这一句疑似应为
"考虑到这时kp与q必然互质"
2015年8月19日 13:56 | # | 引用
嘿嘿 说:
请自行百度快速幂取模算法,这是CS算法中一个比较基本的算法。
2015年10月 7日 16:59 | # | 引用
mentos 说:
太棒!!!!逻辑清晰,描述清楚!感谢博主!真的是三言两语我完全看懂了!还有当时一直就在想能不能由n反推私钥的问题,还有私钥一定能解的证明,真是好感谢!
教材和老师巴拉了一堆我什么都不知道
2015年10月18日 07:31 | # | 引用
哈哈 说:
以 m = kp为例,考虑到这时k与q必然互质这块为什么??
2015年10月22日 17:21 | # | 引用
samaritan 说:
如果事先能找到的目前发现的质数数据集,进行计算出数据库,这样的数据库会有多大。
2015年11月 9日 16:13 | # | 引用
路人甲 说:
你的意思是在我们生成的密钥对里,并将公钥给了鲍勃,然后鲍勃也将自己生成的密钥对里的公钥给了爱丽丝?
但我们在用 SSH-KEYGEN生成密钥对时,给了鲍勃公钥,鲍勃是怎么将自己的密钥对里的公钥给爱丽丝的?
2015年11月28日 20:58 | # | 引用
Conleyfree 说:
文章很好,学到了,真心感谢,但里面一些图片显示不出来,是否是来源网站被墙的问题呢?
2015年12月12日 16:57 | # | 引用
lambda 说:
2015年12月29日 17:54 | # | 引用
iamzken 说:
2016年1月20日 17:18 | # | 引用
zzzp 说:
应为: 17x-3120y=1
2016年1月23日 06:52 | # | 引用
zzzp 说:
d=2753 k=15.
2016年1月23日 06:53 | # | 引用
qwer 说:
y = -k
两项相加的话好像才可以满足扩展欧几里德算法的要求 ax+by = gcd(a, b)
2016年1月25日 09:43 | # | 引用
braintaust 说:
k与q必然互质,
原因是m小于n,m取整数,所以m必然为kp或是kq
同时得到m为kp(k小于q),n为kq(k小于p)
取m为kp,由于q是质数,k小于q,k与q互质
我的理解
2016年2月16日 18:37 | # | 引用
matcloud 说:
阮老师,你看云文档有处公式写错了:使用公钥加密的公式.
2016年3月12日 11:21 | # | 引用
ramsey 说:
有个问题:
因为决定是否能够破解的关键在分解n=p×q,而您提到目前最大的是破解到768位,是否意味着768位(包括768)位以下RSA加密的都已经是不安全的了?
2016年4月13日 14:42 | # | 引用
hacker 说:
看懂了原理,数论知识也看懂了大概,不过博主真牛!
2016年4月28日 10:48 | # | 引用
sherlook 说:
我用python算 65^17 mod 3233 = 2790 你matlab用错了吧
2790^2753 这个值计算机当然算的出来,python算了一下,结果占了我半个屏幕。。。
2016年5月13日 15:52 | # | 引用
李耀东 说:
这个不对称算法绝对是有漏洞的!根据已知e17和n模3233可以算得d=1193 虽然我不知道真的d为3233但是可以等效算出加密值!其实这个基于的是素数的耦合!既自然数的n次幂mod一个素数=自然数本身 而求出那个幕与素数的关系的这个数学推论我感觉可以写个猜想
2016年5月18日 10:34 | # | 引用
Bruce 说:
好文章,感谢。
2016年6月27日 14:12 | # | 引用
HuKeping 说:
你可以把 (m^e -kn)^d 这个等式展开,形式为: C(d,0) * m^ed * (kn)^0 + C(d,1) * m^e(d-1) * (kn)^1 + ...
所以只有一项是不包含kn的,而所有包含n的项在对n取余的操作中都可以消掉。因此得出了那个结论
2016年8月10日 11:29 | # | 引用
胡帆 说:
在第二种m与n不互质的情况下,只有当m小于n时,才会有k与q互质。否则若m大于n,则k值可取成q的倍数,这时却也依然满足m与n不互质的前提条件。
2016年8月13日 22:52 | # | 引用
neo1218 说:
(me - kn)d ≡ m (mod n) 它等同于求证 med ≡ m (mod n)
有大神可以解释一下吗?
2016年8月30日 17:29 | # | 引用
neo1218 说:
哦,我看到了
2016年8月30日 17:30 | # | 引用
Solid 说:
你可以百度一下《100万以内的质数》这篇文档,word文档有几十页。而100万大约是20位左右的样子。自行想象1024位的质数有多少个。大概会是那篇文档的2^1000倍
2016年8月30日 22:53 | # | 引用
地狱鬼才 说:
m^e = c (mod n) 不应该是 m^e = n*k + c 么? 65^17 = 2790 (mod 3233) k=1才是2790 纠结
2016年10月26日 17:30 | # | 引用
yy 说:
[(kp)q-1]h(p-1) × kp ≡ kp (mod q)
这个不对啊,,如果kp大于q呢??
2016年11月11日 16:50 | # | 引用
yy 说:
这里只能是m和N互质,也就是m的域最好选定为m
2016年11月11日 18:34 | # | 引用
程亮 说:
看完后懂RSA的加密原理了,感谢!
2016年11月29日 00:47 | # | 引用
请详细解答 说:
在:
“(2)m与n不是互质关系”这段中,
进一步得到
[(kp)^q-1]^(h(p-1)) × kp ≡ kp (mod q)
请问这是如何得到的?
2016年12月 1日 00:24 | # | 引用
drel 说:
写的很明了:步骤很清晰,不便详细讲述的方法性的步骤也提供了链接!非常感谢!
2016年12月 4日 10:22 | # | 引用
Algeron 说:
好文,由浅入深,公钥和密钥的生成大概理解了。
可还是不懂,具体是怎么加密的。
比如,现在甲要给乙发送一串字符串:“hello”,具体是怎么使用生成的公钥加密这段字符串,又是怎么使用私钥解密的。
2016年12月18日 19:40 | # | 引用
Algernon 说:
明白了,最后的部分没仔细看。
2016年12月18日 20:06 | # | 引用
Colorful 说:
关于d的求法 那里应该有无数个解 这里取的是特解吧, 那到底应该如何算出d呢
2016年12月23日 09:46 | # | 引用
余半仙 说:
都看懂了,学渣大学考试周路过
2016年12月29日 23:01 | # | 引用
斯文一派 说:
请问一下,在加密过程中,通过m^e ≡ c (mod n)来找到c,
则6517 ≡ 2790 (mod 3233) ==> c = 2790。
那么,根据同余的性质,c肯定不唯一,kc也能满足结果,(传递性,a ≡ b (mod m),b ≡ c (mod m),则a ≡ c (mod m))
为何确定c为2790呢?
2017年1月 4日 17:04 | # | 引用
frozone 说:
这是为了下一步构造出来的,问题倒不大;
倒是下一步(kp)^ed ≡ kp (mod q)是不严谨的,写成
(kp)^h(ed) ≡ kp (mod q)更好。
2017年1月16日 10:01 | # | 引用
bianchx 说:
反过来也是单向的。只是人物的昵称换了
2017年2月15日 18:20 | # | 引用
maicss 说:
公钥和私钥的数据都采用ASN.1格式表达
这个表达的实例链接失效了
2017年2月20日 21:00 | # | 引用
ffbh 说:
66666666好详细,一直想知道rsa原理,今天终于明白了,感谢博主无私分享
2017年3月 3日 14:54 | # | 引用
eureka 说:
由这个式子: ed - 1 = kφ(n)
推导出的应该是:
ex - φ(n)y = 1
而不是:
ex + φ(n)y = 1
的呀?
2017年3月21日 13:21 | # | 引用
Sha 说:
牛逼,附上代码就更好啦
2017年3月22日 13:41 | # | 引用
cfzhang 说:
精彩!!我看到原来破根据rsa的公钥破解私钥本质上是一个大整数的质因数分解问题!我惊呆了!吓的我赶紧去分解质因数了,发现没软用。。。目前能破768bit二进制对应的整数。更别说某些场合用的是2048位bit二进制数。。
正纳闷,我拿到私钥加密的数字,怎么解出我的秘钥m,然后果然是一个加密一个解密规则,密不可分,学习了!
2017年4月 7日 17:41 | # | 引用
cfzhang 说:
2017年4月 7日 17:49 | # | 引用
cfzhang 说:
评论内容超过文章内容,可见文章含金量和受欢迎程度。
2017年4月 7日 17:52 | # | 引用
qy_jasmine 说:
2017年4月26日 17:25 | # | 引用
奔跑西红柿 说:
@qy_jasmine:
不需要那么多次计算啊,知道e=17、n=3233、c=2790、设m从1开始++,只需要实验65次,就能找到对应c=2790这个m值了,不需要私匙也可以截获信息m啊。只要知道他们发送的每次是什么值,并且知道公匙就行了啊。大神给解释一下,还是感觉似懂非懂呢?
2017年5月16日 14:22 | # | 引用
sharmin 说:
爱丽丝回复,即是爱丽丝发送信息给鲍勃。因此,你反过来看,即是爱丽丝使用鲍勃的公钥加密,鲍勃使用自身私钥解密。你需要知道,通信双方都应邮寄一对密钥,即公钥和私钥。
2017年5月18日 14:51 | # | 引用
焰 说:
不需要邮寄私钥,两人互相邮寄公钥就可以了(公钥被监听到也没关系),然后彼此用对方的公钥加密信息传送给对方,收到信息的人用自己的私钥解密信息就可以了。
2017年5月25日 15:26 | # | 引用
xucg 说:
第一篇文章用的ab,这篇文章改成了ex,建议统一起来,这样就更通顺了。
2017年6月 1日 18:17 | # | 引用
小马 说:
m与n互质时,mφ(n) ≡ 1 (mod n)怎么推导出(mφ(n))h × m ≡ m (mod n)
2017年6月 3日 18:58 | # | 引用
hello 说:
模不一样!
2017年6月18日 22:53 | # | 引用
卡卡 说:
首先感谢博主的文章 ,非常受益。
只是
不太明白:
(m^e - kn)^d = m (mod n)
这一步如何转化成了
m^ed = m (mod n)
这一步的希望帮忙推理.
谢谢
2017年7月 3日 11:44 | # | 引用
马甲嘎嘎 说:
hi,我有个疑问:程序要计算大数的幂次方,是怎么计算的?比如本文中的例子 2790的2753次方(2790^2753 ) 是怎么计算的呢?我用ptyhon,js,c 都计算不出来,希望解惑!
2017年7月 4日 16:06 | # | 引用
q 说:
請問 2790**2753 ≡ X (mod 3233) 要如何算X,都給出無窮大沒辦法計算
2017年7月10日 11:57 | # | 引用
wuxx 说:
阮老师好,请问根据上一篇的公式,不是 φ(pq) = pq 吗,为什么φ(61x53)=60x52
2017年7月23日 08:57 | # | 引用
流氓兔 说:
深夜睡不着来看大神文章,发现有个问题。你说公匙是大家都能知道(e和n),然后加密后的内容c,假如被截获了,公匙加密公式就剩一个未知数m……这不是能通过解方程把原文m解读出来吗?……为什么还要去搞d这么麻烦
2017年8月19日 02:38 | # | 引用
lw 说:
φ(pq) = φ(q)*φ(P)
φ(q) = q-1
φ(p) = p-1
2017年8月21日 17:54 | # | 引用
状 说:
那么服务端加密,客户端如何解密?
2017年9月 8日 11:45 | # | 引用
Hz 说:
“数学是万物之源”的别走,你这句话是唯心主义好吗。。
2017年9月12日 11:45 | # | 引用
擦蝌蚪 说:
@shindo:
总算看懂了,看样子大家都对这一块有问题
2017年9月28日 10:02 | # | 引用
Jackxwb 说:
服务器使用客户端产生的公钥跟模加密就可以了
2017年9月28日 11:50 | # | 引用
RainyH2O 说:
有一点没懂,为什么e常常选用65537,网上查到的资料是为了减少加密运算次数,但如果φ(n)恰好是65537的倍数,也就是说φ(n)与e不互质该怎么办?换一个质数么?但是我看网上某些RSA的实现直接就用了65537,没加上检测和替换的步骤,还是说有什么理论保证了φ(n)一定不是65537的倍数呢?
2017年10月10日 01:18 | # | 引用
温酒斩近平 说:
服务端发送的加密数据,客户端如何解密?
2017年10月17日 13:43 | # | 引用
nafe 说:
2017年10月17日 14:21 | # | 引用
Phper 说:
真的讲的太好了!感谢阮生的分享
2017年11月 6日 10:47 | # | 引用
sunhk 说:
通过程序的辗转相除法来计算:17x + 3120y = 1 方程解为:(-367, 2)
2017年12月 5日 16:14 | # | 引用
ywqqqqq 说:
你把解代入进去验证等式了吗?
2018年1月 2日 16:01 | # | 引用
KB260 说:
就算没看到具体的证明过程,但还是受益良多。。。
2018年1月12日 16:01 | # | 引用
边宏飞 说:
这是我用阮哥的RSA理论实现的源代码。
http://blog.csdn.net/bian_h_f612701198412/article/details/79358771
欢迎大家指导
2018年2月25日 21:49 | # | 引用
沈琦斌 说:
您好,我刚开始想的时候也没有想明白,还自己计算φ(222)了,后来想明白了。7的222次方=7的220次方*7的2次方;7的220次方各位是1,7的平方各位是9,相乘个位是9。再往后的数学证明就不太明白了。
2018年3月 7日 09:41 | # | 引用
jiahe 说:
你这是对称密码的攻击方式
2018年3月 9日 15:20 | # | 引用
tbswang 说:
这个二元方程的解是不唯一的, 辗转相除法只是算出了其中的一个解.wiki的解释,
https://zh.wikipedia.org/wiki/%E6%A8%A1%E5%8F%8D%E5%85%83%E7%B4%A0
x一般取最小正整数解, 所以, x = x+kn = -367+1*3120 = 2753, 所以, y= -15.
2018年4月13日 11:33 | # | 引用
tomix 说:
'''
将c代入要我们要证明的那个解密规则:
(m^e - kn)^d ≡ m (mod n)
它等同于求证
m^(ed) ≡ m (mod n)
'''
我一开始没懂,百度了一下,这里面应该是用到了这个公式(a^b) % p = ((a % p)^b) % p
2018年4月29日 12:33 | # | 引用
张延勇 说:
前端技术中无法做到私钥加密,公钥解密吗?求阮大大帮帮忙,有点急。。。很是感谢..
2018年5月28日 17:10 | # | 引用
小囧子 说:
已知 e=17, φ(n)=3120,
17x + 3120y = 1
这个方程可以用"扩展欧几里得算法"求解,此处省略具体过程。总之,爱丽丝算出一组整数解为 (x,y)=(2753,-15),即 d=2753。
扩展欧几里得的解不是有无数个吗, 我要是选一个d很大,不也可以防止破解吗,这也只能暴力破解吧
2018年6月 4日 20:43 | # | 引用
Nisen 说:
感谢分享,真是深入浅出受益良多
2018年6月12日 15:23 | # | 引用
abigail 说:
赞!写的真好!跟看精彩的小说一样过瘾!
2018年6月13日 11:02 | # | 引用
HW 说:
[(kp)q-1]h(p-1) × kp ≡ kp (mod q)
这个部分我想了一下貌似有点问题,
前面一步提到
(kp)^(q-1) mod q =1 ---费马小定理
然后可以得到
[(kp)^(q-1)]^(h(p-1)) mod q = 1 --因为取模运算的运算规则,很容易得到这个部分
但是,这个怎么推出
[(kp)^(q-1)]^(h(p-1)) * kp mod q = kp???
这个成立的前提条件是 kp mod q = kp, 我们只知道 gcd(kp,q) = 1, 但这个不等于 kp mod q = kp 吧
这步不是很理解,希望有人解释一下
2018年6月26日 04:41 | # | 引用
HW 说:
这里我把我当M与n不是互质的情况的证明写一下,有不对的地方可以讨论,虽然我以后可能不会回来看了
当M与n不互质时,由于n=p*q, 那么 gcd(M,n) = p 或者 gcd(M,n)=q,跟阮老师在这里假设的一样,我假设 M = k1*p
此时,k1 必然与q互质,不然M会变成pq*k,这样M会被n直接整除
(1)根据费马小定理,当M与q互质时,我们可以得到 M^(q-1)%q = 1
(2)由取模运算的运算规则 a^b %q = (a%q)^b %q
[M^(q-1)]^[k2(p-1)] % q = 1
(3)因为 (p-1)(q-1) = φ(n), ed = k2φ(n)+1这个不懂的请往上翻到φ(n)的推导处,很清楚
所以我们得到 M^(ed-1) % q = 1
(4)改写这个等式到:
M^(ed-1) = k3*q +1
两边乘上 M,得到
M^(ed) = k3*qM +M
(5)我们在之前假设 M = k1p
所以,得到 M^(ed) = k3*q*k1*p +M
M^(ed) = k1k3 *(pq)+M
因为 p*q=n
所以 M^(ed) = k1k3 * n + M
也就是 M^ed mod n = M
得证!
2018年6月26日 05:20 | # | 引用
乔则铈 说:
第九个的子标题(2)“m必然等于kp或kq”不对啊,根据举例,m是65,p是61,q是53,不对啊?
2018年7月10日 12:20 | # | 引用
qing 说:
看到有留言说客户端如果要发消息给服务端怎么办?怎么保证加密,当然,客户端可以发公钥给服务端,但是不是通常的做法。
以HTTPS中ssl的做法为例子,其实通信的主体还是以对称加密为主,
1.客户端拿到服务器的公钥x
2.客户端随机生成一串字符串y,并用x加密变成y`发送给服务器。
3.服务器端拿到加密之后的y`用私钥q解密,得到y。
4.此时服务器和客户端都拿到了一个y,而且是在安全的状态下交换了这个y。
5.之后的通信都是用这个y做对称加密。
2018年7月30日 17:32 | # | 引用
bobjiao 说:
为什么不设t=t'k?
2018年8月13日 19:25 | # | 引用
zxy 说:
为什么m必须小于n
2018年9月21日 15:11 | # | 引用
zxy 说:
了解了。为什么m必须小于n
在第二种m与n不互质的情况下,只有当m小于n时,才会有k与q互质。否则若m大于n,则k值可取成q的倍数,这时却也依然满足m与n不互质的前提条件。
2018年9月21日 15:12 | # | 引用
高中生 说:
ex + φ(n)y = 1
写成
ex - φ(n)y = 1
更好吧.
2018年9月29日 15:13 | # | 引用
arainer 说:
同问,文章这里应该写的不对
2018年10月10日 10:45 | # | 引用
lyman 说:
为什么私钥d必须为正整数才行
2018年11月 8日 14:50 | # | 引用
jsee 说:
弄懂同余再说吧朋友
2018年11月 9日 17:50 | # | 引用
代文朱 说:
因为m n 是不是互质关系并且n是两个两个质因数的乘积,那么m的因数必然包含n的质因数p或者q
2018年12月27日 00:37 | # | 引用
Peng 说:
(1)根据费马小定理,当M与q互质时,我们可以得到 M^(q-1)%q = 1
(2)由取模运算的运算规则 a^b %q = (a%q)^b %q
[M^(q-1)]^[k2(p-1)] % q = 1
这个(2)引用的是不是不对啊,应该是根据a≡1mod(n),所以a^b≡1mod(n)吧
所以M^(q-1)≡1mod(n)时,(M^(q-1))^(p-1)≡1mod(n)
2019年1月 9日 01:10 | # | 引用
Peng 说:
(2)由取模运算的运算规则 a^b %q = (a%q)^b %q
[M^(q-1)]^[k2(p-1)] % q = 1
这个(2)引用的是不是不对啊,应该是根据a≡1mod(n),所以a^b≡1mod(n)吧
所以M^(q-1)≡1mod(n)时,(M^(q-1))^(p-1)≡1mod(n)
2019年1月 9日 01:10 | # | 引用
jonkee 说:
(2)m与n不是互质关系。
此时,由于n等于质数p和q的乘积,所以m必然等于kp或kq。
m不是表示待加密的數據嗎?待加密的數據不是完全不可預測的嗎?
為什麼說“m必然等于kp或kq”?
2019年5月31日 17:55 | # | 引用
PPD 说:
我可能太笨
```
m与n互质。根据欧拉定理,此时 mφ(n) ≡ 1 (mod n)得到 (mφ(n))h × m ≡ m (mod n)
```
这个推导都没搞懂。
请小伙伴解释一下,谢谢~
2019年6月12日 17:43 | # | 引用
lizhifeng 说:
设 m^$(n) = kn + 1 则 m^($(n)h+1) % n = (kn+1)^h * m % n = m % n 。 多项式展开你不会么?
2019年9月16日 15:21 | # | 引用
Chen Jianhui 说:
对于(2)m和n不是互质的情况,是不是需要考虑m是n的倍数的情况?尽管m^ed ≡ m (mod n)也是成立的
另外后面的证明可不可以这样,(kp)^ed ≡ kp (mod q), (kp)^ed ≡ kp (mod p) => (kp)^ed ≡ kp (mod [p,q]) => m^ed ≡ m (mod n), [p,q]表示p和q的最小公倍数。
2019年10月16日 11:40 | # | 引用
大熊有点飘 说:
等式左边是kp的ed次方,tq=kp的ed-1次方,p是tq的因数,q与p互质,所以t必然是p的倍数
2019年12月12日 17:01 | # | 引用
大熊有点飘 说:
根据欧拉定理,mφ(n)可以表示为kn+1,mφ(n)的h次方为kn+1的h次方,然后把左边的多项式展开后,发现为m加上n的各种倍数,被n除,余数只能是m
2019年12月12日 17:27 | # | 引用
young 说:
峰哥,我利用拓展欧几里得算法求得 17x + 3120y = 1,x = -367, y = 2,想问下,私钥一对整数都必须是正整数吗?
2020年2月26日 16:46 | # | 引用
zl 说:
[(kp)q-1]h(p-1) × kp ≡ kp (mod q)
这个是怎么得出来的啊??
2020年3月22日 16:53 | # | 引用
Dani 说:
第五步,计算e对于φ(n)的模反元素d。
--- 是不是意味了已知公钥(e,n)可以算出私钥(d,n) ???
2020年5月12日 11:08 | # | 引用
hello 说:
是的,服务端然后用私钥解密即可
2020年5月29日 15:37 | # | 引用
才搞懂 说:
同一把公钥,对相同的数据,进行加密操作,发现每次加密的最终的密文是不一样的。
2020年8月26日 17:11 | # | 引用
CHJ吉吉 说:
d是不是可以有多个解?d能有多个解不就等于密钥可以有多个?
2020年11月14日 09:47 | # | 引用
testqqqq 说:
有个问题,关于e d,e是随机生成,但是d是e的模反,那么(e,d)这一对就不是唯一的咯?根据第一部分RSA算法原理的来说,b+kn 都是a的模反?
2020年11月22日 06:42 | # | 引用
zerolei 说:
回顾上面的密钥生成步骤,一共出现六个数字:
p 61
q 53
n = 61×53 = 3233
φ(n) φ(3233)等于60×52,即3120。
e和d 17与2753 或103与727
----------
在文章中,私钥1(n,d)即(3233,2753), 公钥1(n,e)即是 (3233, 17);
6个数的最后两个的顺序是先确定e在推算出d,
这里有问题,应该先确定私钥中的d,再推算出e:d可以取多个值,例如727,可得出另一套私钥和公钥
私钥2(n,d)即(3233,727),公钥2(n,e)即是 (3233, 103)
2021年1月14日 16:44 | # | 引用
n 说:
查了下RSA算法,加密通信需要双方交换公钥的呀。
没想明白客户端是怎么做的,成千上万的客户端都跟服务端交换公钥 感觉不现实。
对于这种一对多的服务,RSA在实际中是怎么应用的呢?
2021年3月26日 17:04 | # | 引用
WhXcjm 说:
完全理解,受益匪浅,感谢
2021年4月27日 20:40 | # | 引用
liuzx 说:
n一定得是两个质数之积吗?我看算法原理好像只要能求出φ(n) = (p-1)就可以实现
2021年5月 4日 08:10 | # | 引用
拉边 说:
http://blog.csdn.net/bian_h_f612701198412/article/details/79358771
这是我实现的完整版的RSA算法,代码非常简单
2021年6月26日 19:46 | # | 引用
ked1876 说:
ed ≡ 1 (mod φ(n)) 正确的应该是 ed ≡ 1 (mod n)
2022年5月 1日 18:40 | # | 引用
XornTan 说:
刚刚搜资料发现这篇文章是13年我生日时候发表的,22年生日刚过就搜到了,缘分啊
2022年7月 5日 16:55 | # | 引用
hys 说:
以 m = kp为例,考虑到这时k与q必然互质,则根据欧拉定理,下面的式子成立:
应该是 m与q必然互质
2023年1月10日 01:49 | # | 引用
none 说:
RSA的好处:
坏处:
2023年1月24日 12:28 | # | 引用
Stan 说:
因数分解 应该改为 质因数分解吧! 只有分解成质因数才有意义
2023年3月 5日 17:31 | # | 引用
CCHL 说:
像这样的高质量的blog难寻,我自己也写了些blog向前辈学习
2023年6月 5日 11:16 | # | 引用
顺 说:
“另一种是先选择一种"对称性加密算法"(比如DES),用这种算法的密钥加密信息,再用RSA公钥加密DES密钥。”
这就是https的方式
2023年7月20日 11:22 | # | 引用
lizhi 说:
这就涉及到PKI认证体系,可以参考HTTPS
2023年11月14日 17:58 | # | 引用
zff2023 说:
第一步,随机选择两个不相等的质数p和q。
爱丽丝选择了61和53。(实际应用中,这两个质数越大,就越难破解。)
有个问题,这里两个质数p和q从哪里取, 是需要先保存一批质数然后随机获取吗
2024年3月29日 15:41 | # | 引用