你是否想过,计算机为什么会加减乘除?或者更直接一点,计算机的原理到底是什么?
Waitingforfriday有一篇详细的教程,讲解了如何自己动手,制作一台四位计算机。从中可以看到,二进制、数理逻辑、电子学怎样融合在一起,构成了现代计算机的基础。
一、什么是二进制?
首先,从最简单的讲起。
计算机内部采用二进制,每一个数位只有两种可能"0"和"1",运算规则是"逢二进一"。举例来说,有两个位A和B,它们相加的结果只可能有四种。
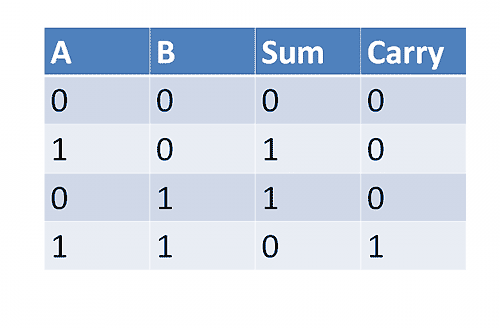
这张表就叫做"真值表"(truth table),其中的sum表示"和位",carry表示"进位"。如果A和B都是0,和就是0,因此"和位"和"进位"都是0;如果A和B有一个为1,另一个为0,和就是1,不需要进位;如果A和B都是1,和就是10,因此"和位"为0,"进位"为1。
二、逻辑门(Logic Gate)
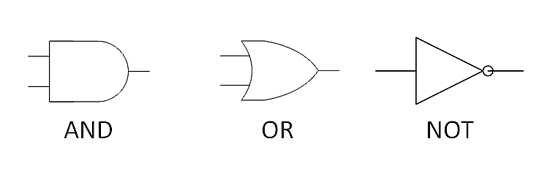
布尔运算(Boolean operation)的规则,可以套用在二进制加法上。布尔运算有三个基本运算符:AND,OR,NOT,又称"与门"、"或门"、"非门",合称"逻辑门"。它们的运算规则是:
AND:如果( A=1 AND B=1 ),则输出结果为1。
OR:如果( A=1 OR B=1 ),则输出结果为1。
NOT:如果( A=1 ),则输出结果为0。
两个输入(A和B)都为1,AND(与门)就输出1;只要有任意一个输入(A或B)为1,OR(或门)就输出1;NOT(非门)的作用,则是输出一个输入值的相反值。它们的图形表示如下:
三、真值表的逻辑门表示
现在把"真值表"的运算规则,改写为逻辑门的形式。
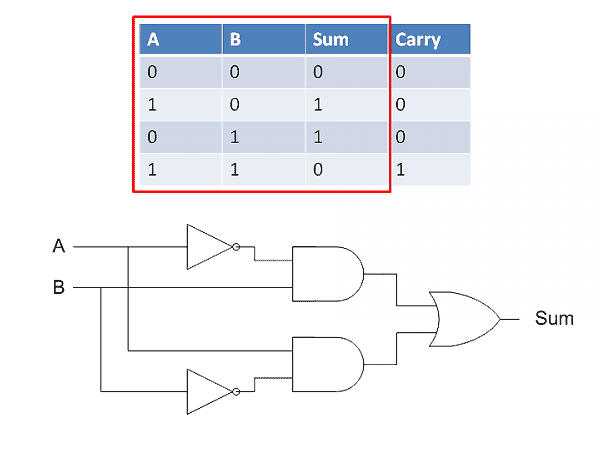
先看sum(和位),我们需要的是这样一种逻辑:当两个输入不相同时,输出为1,因此运算符应该是OR;当两个输入相同时,输出为0,这可以用两组AND和NOT的组合实现。最后的逻辑组合图如下:
再看carry(进位)。它比较简单,两个输入A和B都为1就输出1,否则就输出0,因此用一个AND运算符就行了。
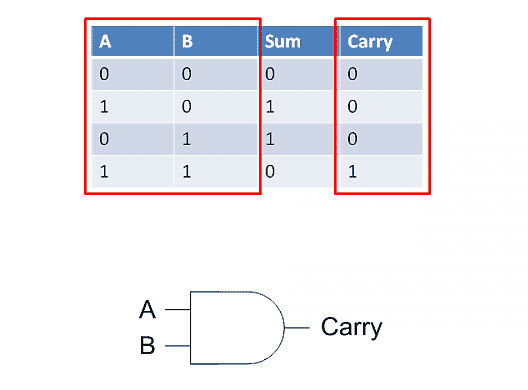
现在把sum和carry组合起来,就能得到整张真值表了。这被称为"半加器"(half-adder),因为它只考虑了单独两个位的相加,没有考虑可能还存在低位进上来的位。
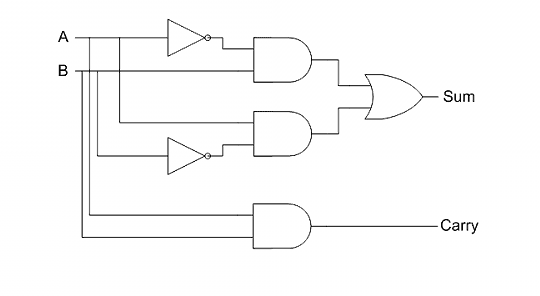
四、扩展的真值表和全加器
如果把低位进上来的位,当做第三个输入(input),也就是说,除了两个输入值A和B以外,还存在一个输入(input)的carry,那么问题就变成了如何在三个输入的情况下,得到输出(output)的sum(和位)和carry(进位)。
这时,真值表被扩展成下面的形式:
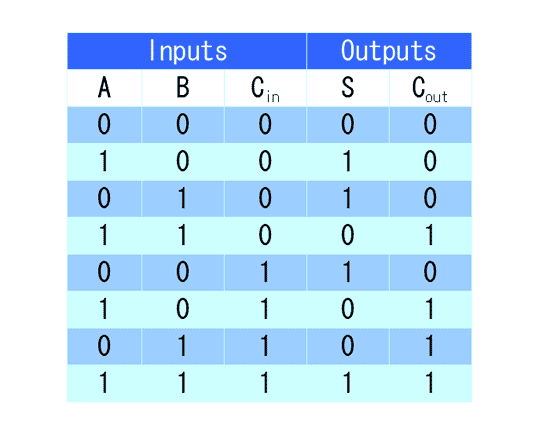
如果你理解了半加器的设计思路,就不难把它扩展到新的真值表,这就是"全加器"(full-adder)了。
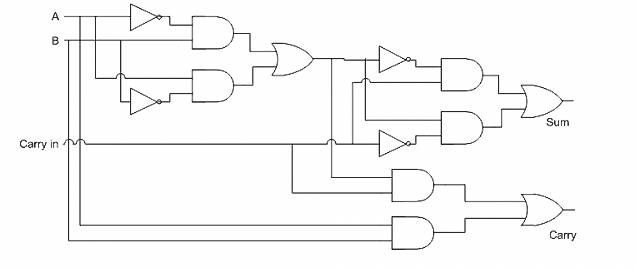
五、全加器的串联
多个全加器串联起来,就能进行二进制的多位运算了。
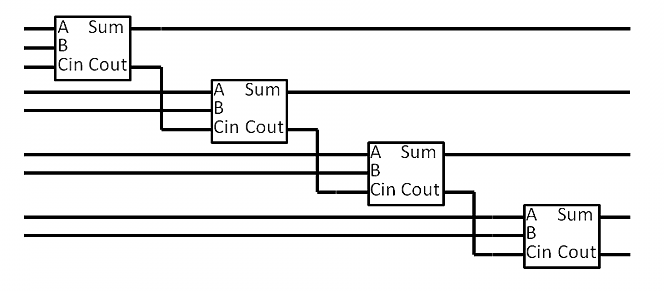
先把全加器简写成方块形式,注明三个输入(A、B、Cin)和两个输出(S和Cout)。
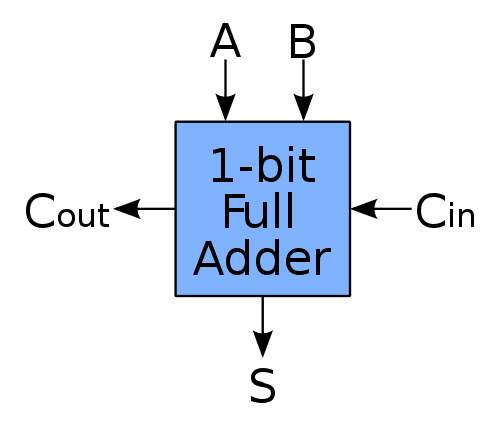
然后,将四个全加器串联起来,就得到了四位加法器的逻辑图。
六、逻辑门的晶体管实现
下一步,就是用晶体管做出逻辑门的电路。
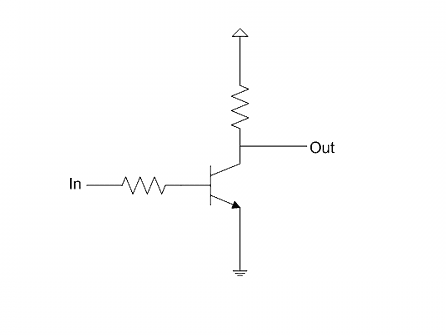
先看NOT。晶体管的基极(Base)作为输入,集电极(collector)作为输出,发射极(emitter)接地。当输入为1(高电平),电流流向发射极,因此输出为0;当输入为0(低电平),电流从集电极流出,因此输出为1。
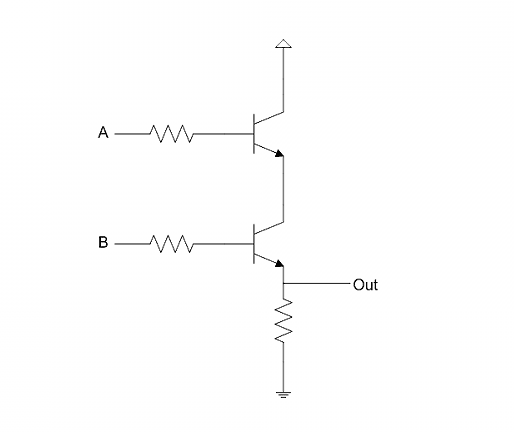
接着是AND。这需要两个晶体管,只有当两个基极的输入都为1(高电平),电流才会流向输出端,得到1。
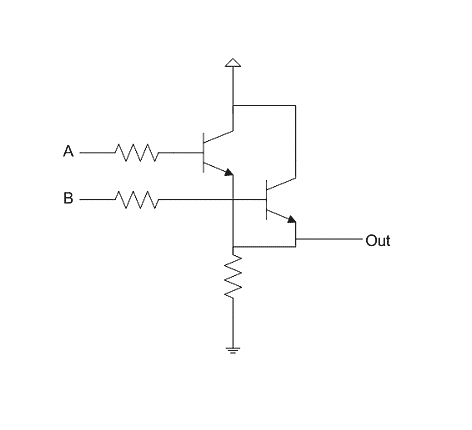
最后是OR。这也需要两个晶体管,只要两个基极中有一个为1(高电平),电流就会流向输出端,得到1。
七、全加器的电路
将三种逻辑门的晶体管实现,代入全加器的设计图,就可以画出电路图了。
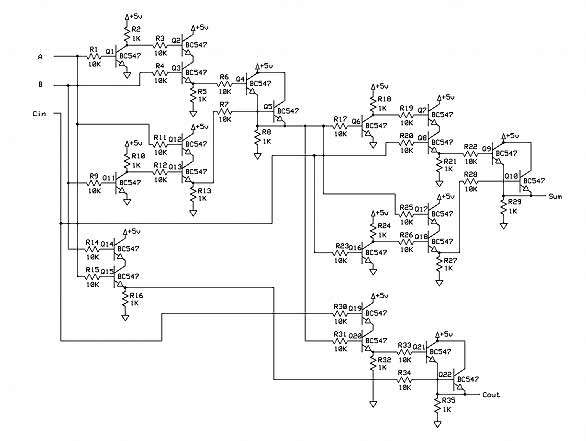
(点击看大图)
按照电路图,用晶体管和电路板组装出全加器的集成电路。

左边的三根黄线,分别代表三个输入A、B、Cin;右边的两根绿线,分别代表输出S和Cout。
八、制作计算机
将四块全加器的电路串联起来,就是一台货真价实的四位晶体管计算机了,可以计算0000~1111之间的加法。

电路板的下方有两组各四个开关,标注着"A"和"B",代表两个输入数。从上图可以看到,A组开关是"上下上上",代表1011(11);B组开关是"上下下下",代表1000(8)。它们的相加结果用五个LED灯表示,上图中是"亮暗暗亮亮",代表10011(19),正是1011与1000的和。
九、结论
虽然这个四位计算机非常简陋,但是从中不难体会到现代计算机的原理。
完成上面的四位加法,需要用到88个晶体管。虽然当代处理器包含的晶体管数以亿计,但是本质上都是上面这样简单电路的累加。
(完)


membogg 说:
又有新东西学习啦
2011年3月12日 22:30 | # | 引用
咨询顾问 说:
深入浅出。谢谢阮工
2011年3月12日 22:33 | # | 引用
lanisle 说:
阮老师,正需要这个,谢谢您的文章,:)
2011年3月12日 22:50 | # | 引用
ufo 说:
明白了通过3极管物理特性>实现布尔逻辑>再实现二进制加减乘除
利用二进制加减乘除运算的极其简单性来实现我们常用的10制运算
2011年3月12日 23:09 | # | 引用
氢气球 说:
把大学里的《模拟电子电路》和《数字电路》学好了,也就知道了。
2011年3月13日 00:11 | # | 引用
gelosie 说:
坊间野史, 当年发明内存的时候,也是用几位的,没实用意思的设计去申请专利~~
2011年3月13日 03:57 | # | 引用
NIX 说:
通俗易懂,又要把多少人“带进”计算机的世界呀!是喜是悲?
2011年3月13日 10:07 | # | 引用
水水 说:
怀念大学时的数电生活
2011年3月13日 10:17 | # | 引用
慢羊羊 说:
需要指出的是,现在大部分电路采用的是场效应晶体管,三极管由于能耗太大,只应用于一些比较特殊的电路。
2011年3月13日 11:58 | # | 引用
xt 说:
呵呵,这个正是我大二在《数字电子技术基础》课上学过的内容
2011年3月13日 13:30 | # | 引用
aaa 说:
来提意见。一峰的日志近来全是转载原创太少了……(虽然我欣赏辛勤的翻译)
还有含盖面太广了,这样大多方面就成了浅尝即止使blog变得更像一个it新闻站
2011年3月13日 14:37 | # | 引用
ybsolar 说:
哪里能搞到这样的电路板,我也想自己弄一个玩玩!
2011年3月13日 15:50 | # | 引用
文盲 说:
感觉犹如时光倒返7年,回到偶大一的时候。
2011年3月13日 17:37 | # | 引用
LP 说:
Charles Petzold的书《编码的奥秘》应该是讲解这方面的翘楚了。
http://book.douban.com/subject/1024570/
2011年3月13日 19:21 | # | 引用
xh 说:
黑客与画家 什么时候出版?
2011年3月13日 20:48 | # | 引用
floyd 说:
这种板子可以自己热转印,就是比较伤打印机,很多打印店不给打
2011年3月13日 21:31 | # | 引用
aaa 说:
传统方法是用覆铜板和三氯化铁。
2011年3月14日 12:32 | # | 引用
Haocheng 说:
好像很麻烦的样子...用FPGA模拟不是更方便么?
2011年3月14日 14:11 | # | 引用
Sharling 说:
同。。文中完全用模拟芯片来实现逻辑运算显得更加犀利``
2011年3月15日 00:22 | # | 引用
fbcon 说:
用Minecraft模拟16位算术逻辑单元 http://www.youtube.com/watch?v=LGkkyKZVzug
2011年3月15日 22:20 | # | 引用
myzerg 说:
不学计算机的看不懂看不下去,学得看了又太简单,
这文章写得意义是什么?
2011年3月16日 18:07 | # | 引用
城主 说:
这个我们玩过。。
2011年3月18日 00:05 | # | 引用
Necolo 说:
这个我在英国大学预科就学掉了.....
2011年3月18日 07:51 | # | 引用
gordon 说:
帅哥,你把开关和LED发光二级管换成键盘和显示器就是标准输入和标准输出了。
还可以钣金做一个机箱的壳子。
这样一台简单的具有键盘、显示器和机箱的计算机就诞生了。
oh,yeah。that's cool.
网上还有个哥们用导线做CPU的,我操,一个大盒子。
一台非集成电路的计算机诞生了,土法上马,真土,土的掉渣。
2011年3月19日 08:46 | # | 引用
gordon 说:
上面有很多同学说学过《模拟电路》和《数字电路》的都明白,我可以这么清晰的说,除非你是电子专业的,或者说学过《信号与系统》这门课,不然狗屁,竟然把《模拟电路》和《数字电路》学懂了。
这两门课所以难难,其实是对老师就是一个挑战,很多老师都讲不清楚为什么,当然数电是好理解一点,但是你没有和信息(或者说信号)的传输、放大、处理联系起来。
反正计算机专业的《数字电路》《模拟电路》开得是很垃圾,因为如果要讲明白要有前置课程的,而在电子专业《信号与系统》这门课本来就是难点之一。
而且很多老师讲课本来就是为了应付考试,根本就不知道到底怎么回事,反正没把学生讲懂。
2011年3月19日 10:15 | # | 引用
梦之源泉 说:
谢谢阮老师的深入浅出的介绍。
2011年3月21日 10:57 | # | 引用
天天快乐 说:
学计算机的,看到这样的文章很是欣慰。看了大家的评论才知道,数电、模电应该讲过的。大学的课真应该改改了。
2011年3月24日 13:32 | # | 引用
砖家 说:
大学学过,原理也了解,但是自己设计或者讲却讲不出来。
2011年4月 1日 23:00 | # | 引用
yxgu 说:
学过,当年用模拟软件都实现过。
道理很简单,叠加起来复杂了,就麻烦了。
还是需要知道设计原理 和化简原理才行的。
谢谢LZ给了我一些美好的回忆…………
2011年4月23日 00:04 | # | 引用
小丸 说:
计算机的基本原理是如此简单,但真正实现起来困难还是很多的。
2011年5月30日 13:42 | # | 引用
cquwb 说:
那个NOT 门 为什么当输入为0(低电平),电流从集电极流出,因此输出为1。
这个怎么理解 输入为0 是不是就是基极的电压为0了啊 都0了那基极肯定也没有电流
那集电极是哪来的电流啊。。
2011年9月 7日 20:16 | # | 引用
moonracker 说:
太棒了,讲的十分清晰,再看不懂是傻瓜。
中间是导线接的CPU啊。可惜没有个存储器的地儿。
2011年11月15日 11:19 | # | 引用
gad 说:
2012年9月 3日 17:16 | # | 引用
张海鹏 说:
能不能找到一种三极管或者是场效应晶体管的替代,然后重新设计四位计算机?
2014年6月 1日 10:39 | # | 引用
肝火旺 说:
我用proteus照着做了,不好使,求解答
2014年7月25日 13:33 | # | 引用
温发裕 说:
那么如何实现软件控制啊
2014年10月 7日 08:47 | # | 引用
wayne 说:
这是四位计算机,如果想要32位或者64位的计算机,是不是就只需要在第五步“全加器的串联”中串联到32个或者64个就行了?
求解答,谢谢
2015年2月 1日 11:03 | # | 引用
qwert 说:
非门到底是怎么回事?
2015年5月12日 18:04 | # | 引用
C罗 说:
深入浅出,有助于理解计算机的工作原理;很想动手玩玩
2015年9月14日 12:31 | # | 引用
Frank 说:
求原件和材料清单。新手上路,不知道怎么购买
2016年11月18日 08:41 | # | 引用
zzchina 说:
估计是 NPN 三极管9013, 10K欧姆 ,1k欧姆 三种元件即可, 5v 直流电源.
2016年11月21日 07:28 | # | 引用
turbo 说:
我觉得我看懂了
2017年10月25日 17:29 | # | 引用
Alan 说:
理论上是,所谓几位的计算机说的就是一次能运算多少位元的数据,不过现代计算机(CPU)所说的Bit通常指的是通用寄存器的位数(Bit)
2018年1月27日 17:56 | # | 引用
RaulYang 说:
做个不恰当的比喻,中国大学如果中国足球一般。U17,U21都能与世界强队较量,大学一毕业怎么就落后世界名校那么多。
2018年6月20日 09:18 | # | 引用
P ray 说:
厉害,勾起大一学数电模电的回忆来
2019年2月27日 16:12 | # | 引用
荒原之梦 说:
阮老师比课本上讲得清楚 :-)
2019年7月 8日 21:05 | # | 引用
rangwer 说:
举例来说,有两个位A和B,它们相加的结果只可能有四种。
这句话如果描述为:有两个位A和B,它们有四种相加方式,相加的结果只可能有两种
会不会更好捏。
2019年9月 4日 10:08 | # | 引用
土法炼钢 说:
@gordon:
原理上大概懂,实际要搞的非常明白透彻还是要花大量时间的。内存的原理更难些。
2021年9月13日 16:15 | # | 引用