去年12月，美国康涅狄格州发生校园枪击案，造成28人死亡。
资料显示，1982年至2012年，美国共发生62起（大规模）枪击案。其中，2012年发生了7起，是次数最多的一年。
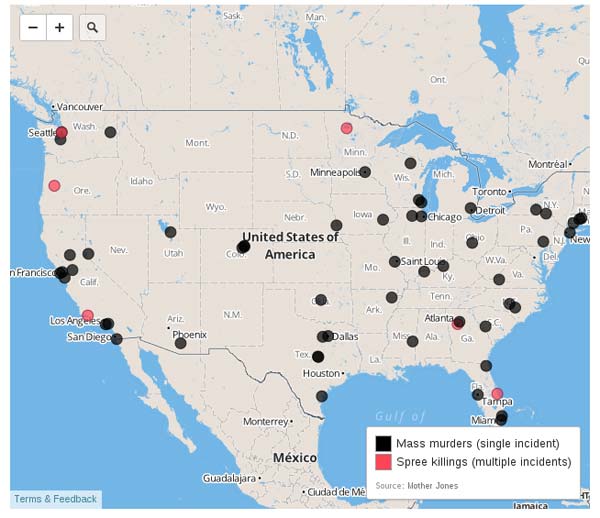
去年有这么多枪击案，这是巧合，还是表明美国治安恶化了？
前几天，我看到一篇很有趣的文章，使用"泊松分布"（Poisson distribution），判断同一年发生7起枪击案是否巧合。
让我们先通过一个例子，了解什么是"泊松分布"。
已知某家小杂货店，平均每周售出2个水果罐头。请问该店水果罐头的最佳库存量是多少？
假定不存在季节因素，可以近似认为，这个问题满足以下三个条件：
（1）顾客购买水果罐头是小概率事件。
（2）购买水果罐头的顾客是独立的，不会互相影响。
（3）顾客购买水果罐头的概率是稳定的。
在统计学上，只要某类事件满足上面三个条件，它就服从"泊松分布"。
泊松分布的公式如下：
各个参数的含义：
P：每周销售k个罐头的概率。
X：水果罐头的销售变量。
k：X的取值（0，1，2，3...）。
λ：每周水果罐头的平均销售量，是一个常数，本题为2。
根据公式，计算得到每周销量的分布：
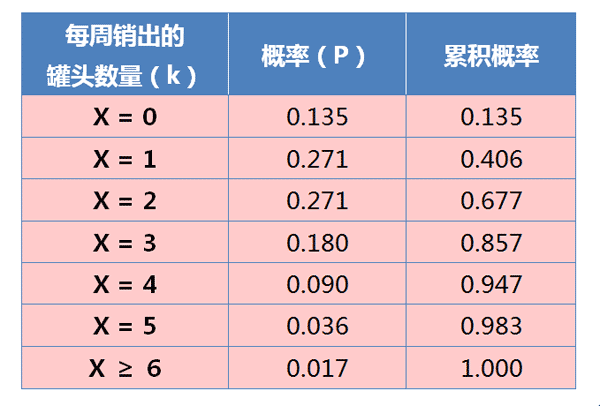
从上表可见，如果存货4个罐头，95%的概率不会缺货（平均每19周发生一次）；如果存货5个罐头，98%的概率不会缺货（平均59周发生一次）。
现在，我们再回过头，来看美国枪击案。
假定它们满足"泊松分布"的三个条件：
（1）枪击案是小概率事件。
（2）枪击案是独立的，不会互相影响。
（3）枪击案的发生概率是稳定的。
显然，第三个条件是关键。如果成立，就说明美国的治安没有恶化；如果不成立，就说明枪击案的发生概率不稳定，正在提高，美国治安恶化。
根据资料，1982--2012年枪击案的分布情况如下：
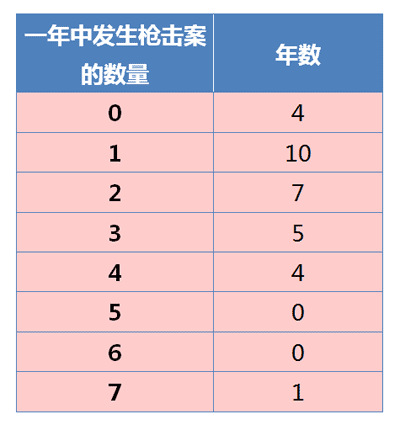
计算得到，平均每年发生2起枪击案，所以 λ = 2 。
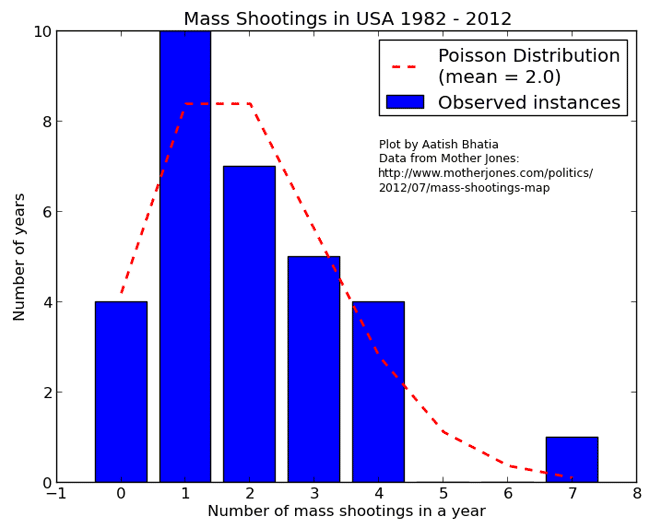
上图中，蓝色的条形柱是实际的观察值，红色的虚线是理论的预期值。可以看到，观察值与期望值还是相当接近的。
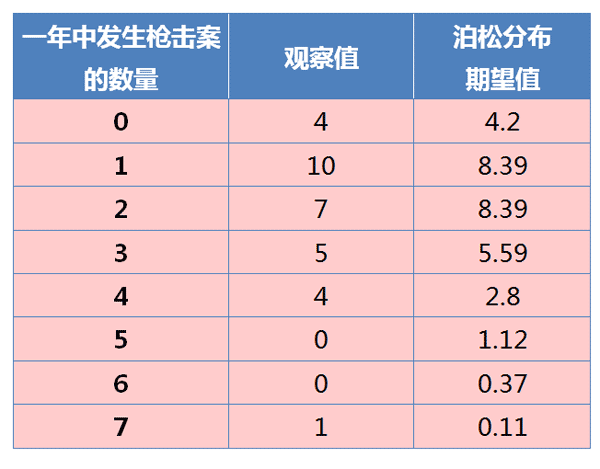
我们用"卡方检验"（chi-square test），检验观察值与期望值之间是否存在显著差异。
卡方统计量 = Σ [ ( 观察值 - 期望值 ) ^ 2 / 期望值 ]
计算得到，卡方统计量等于9.82。查表后得到，置信水平0.90、自由度7的卡方分布临界值为12.017。因此，卡方统计量小于临界值，这表明枪击案的观察值与期望值之间没有显著差异。所以，可以接受"发生枪击案的概率是稳定的"假设，也就是说，从统计学上无法得到美国治安正在恶化的结论。
但是，也必须看到，卡方统计量9.82离临界值很接近，p-value只有0.18。也就是说，对于"美国治安没有恶化"的结论，我们只有82%的把握，还有18%的可能是我们错了，美国治安实际上正在恶化。因此，这就需要看今后两年中，是否还有大量枪击案发生。如果确实发生了，泊松分布就不成立了。
[参考阅读]
* 泊松分布，by 曹亮吉
* 卡方分布（PDF文件）
（完）
御宅暴君 说：
1982年至2012年，美国共发生62起枪击案。
我倒是很吃惊比我想象中的还要少，我以为至少上万，实际却不到百。
2013年1月 8日 22:05 | # | 引用
orvice 说：
马上要考概率，我的眼泪就要掉下来...
2013年1月 8日 22:36 | # | 引用
RedNax 说：
这里所谓枪击案是指大规模枪击案(mass shooting)随便射死一两个那种不算……
2013年1月 8日 22:36 | # | 引用
rexur 说：
我觉得 用泊松分布跟枪击案 跟 cpc历代常委数与泊松分布 一样, 分析起来都是对牛弹琴.
这个模型不是简单随机的, 枪击案的产生数目从社会学上有理由认为是其他因素综合影响的结果,而这些因素可能包括经济(繁荣/危机),科技发展,通货膨胀和油价涨跌,甚至战争等等.
就像有人拟合了一下米国自闭症数目和有机食品推广的90年代后历年指数,发现非常贴近,这能得出一个有意义的结论吗?
2013年1月 8日 23:05 | # | 引用
ChengWei 说：
2013年1月 8日 23:14 | # | 引用
嘉佑 说：
数学真神奇，这也能用得上。
不过看得我满头雾水，看不懂，还好最后有总结。
2013年1月 9日 01:17 | # | 引用
ncsglz 说：
MASS SHOOTING不足以反应治安状况，而应该是普通的谋杀案、抢劫案、00XX案等等
2013年1月 9日 09:16 | # | 引用
CJ 说：
感觉统计学运用到此类社会研究上几乎是没有什么大的帮助的。
这些数字只有微乎其微的参考价值。
令人惊讶的是，整个文章分析下来，对社会治安的状况没有什么有意义的分析和结论，全是数字。
另外，其中
（2）枪击案是独立的，不会互相影响。
我觉得需要论证。比如：社会事件对整个社会人群显然是有心理影响的
其它两个条件只是数字游戏了。
这让我想起了一本书，《技术垄断——文化向技术投降》。
2013年1月 9日 09:45 | # | 引用
StanleyZ 说：
"因此，这就需要看今后两年中，是否还有大量枪击案发生。如果确实发生了，泊松分布就不成立了“
即便今后两年还有枪击案， 也是泊松分布有很大可能不成立吧。
2013年1月 9日 09:48 | # | 引用
未小根 说：
是受到这篇文章的启发吗？http://www.empiricalzeal.com/2012/12/24/are-mass-shootings-really-random-events-a-look-at-the-us-numbers/
2013年1月 9日 09:52 | # | 引用
kk 说：
如果存货4个罐头，95%的概率不会缺货（平均每19周发生一次）；如果存货5个罐头，98%的概率不会缺货（平均59周发生一次）----------------求教，括号里面的内容如何理解？
2013年1月 9日 10:29 | # | 引用
我的大名 说：
数据样本如此之小，这样的分析根本没有意义。
2013年1月 9日 10:51 | # | 引用
横箫斜吹雨 说：
哈哈，概率概率，我当年概率也学得一塌糊涂……
2013年1月 9日 11:19 | # | 引用
reverland 说：
假设检验充满争议……个人不喜欢这种飘渺的方法……
https://en.wikipedia.org/wiki/Statistical_hypothesis_testing#Controversy
2013年1月 9日 12:06 | # | 引用
Jay 说：
如果存货5个罐头，98%的概率不会缺货（平均59周发生一次） -- 应该是49周
2013年1月 9日 13:03 | # | 引用
kk 说：
怎么求得是49周？请赐教。
2013年1月 9日 13:43 | # | 引用
Firefly 说：
2013年1月 9日 15:37 | # | 引用
Firefly 说：
是博主搞错了吧，赶快纠正，不要误导群众。
2013年1月 9日 15:41 | # | 引用
天一 说：
1/(1-0.983)=58.8
2013年1月 9日 16:33 | # | 引用
罗丹 说：
小白问一下，第4张图的图表，最左列应该是k=0，k=1...吧，不应该是X吧？
2013年1月10日 09:31 | # | 引用
bleach 说：
阮一峰您好，个人认为文中存在一些问题。
1.文中的第二个假设（独立性假设）过强，该假设本身就需要先使用独立性检验来验证。
2.文中的做法和文章的目的是不相符的。文章需要验证的问题是“枪击案的发生于相对于时间是独立的（即时间与枪击案的数目没有明显的相关关系）”，而文章中做的是“去除时间维度的信息后，枪击案发生的频数符合”。也就是说，第二条假设其实是文章本来需要论证的内容，而去除时间信息后枪击案数目符合什么分布跟枪击案数目是否有逐年增长的趋势没有关系。
对于第二点可以举个例子，2012-1982年的枪击案数目（注意此处为时间倒序）是： 7,3,1,4,3,4,3,2,1,1,0,1,1,5,3,2,1,1,1,4,2,3,1,2,1,1,1,0,2,0,1。
将此序列重新排序可以得到0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,5,7 或者7,5,4,4,4,3,3,3,3,3,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0。 如果按照文中的方法忽略时间维度的信息进行检验后，这三个序列的结果是一样的，但是如果美国2012-1982年枪击案的数目真的是7,5,4,4,4,3,3,3,3,3,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0的话，那么肯定所有人都会认为枪击案是逐年增长的。
另外可以使用一些非参数的趋势性检验来粗略验证一下枪击案的数目是否随时间呈增长趋势。
2013年1月10日 21:40 | # | 引用
阮一峰 说：
@bleach：
你说得对，第二个假设不一定成立。
我的这篇文章其实写的是，泊松分布不足以推翻这些假设。
2013年1月11日 00:59 | # | 引用
xiaolizi 说：
@bleach：
的确，而且这句“显然，第三个条件是关键。如果成立，就说明美国的治安没有恶化；如果不成立，就说明枪击案的发生概率不稳定，正在提高，美国治安恶化。”也有些片面，不稳定也可能说明治安在变好。
2013年1月11日 13:58 | # | 引用
冰上游鱼 说：
哇 学数学的伤不起啊！
2013年1月12日 19:57 | # | 引用
海纳百川 说：
看这类文章有意思，学到了不少。概率我那时学的不好啊。
2013年1月14日 10:15 | # | 引用
路过的游客 说：
最近在看《基地》系列，这让我想到了心理史学。
2013年1月14日 15:28 | # | 引用
Wei 说：
您的留言让我注意到，文章分析的是大规模枪击和美国治安状况的关联是吗？如果是，及时美国大规模枪击案件在1982年到2012年上升，可以得到美国治安恶化的结论吗？（纯技术探讨，不针对命题本身~）
2013年1月17日 22:13 | # | 引用
yvonne 说：
枪击案是独立的，不会互相影响。
枪击案的发生概率是稳定的。
怎么看都觉得这两个条件不成立！
2013年1月18日 14:12 | # | 引用
AJ 说：
原作者的数据已经更新了，现在是0.09， 不是0.18。
2013年1月20日 11:42 | # | 引用
AJ 说：
觉得美国治安逐年恶化的人可以去FBI 和各个城市的PD网站去看domestic violence 数据，各项指标都显示美国crime 是逐年下降尤其是2000年以来。
另：统计学在criminology 运用不是很少，是很多。
“（2）枪击案是独立的，不会互相影响。”
原文说的不是对普通人社会心理影响，说的是case 同case 之间是独立的，并不是一个罪犯为了对另一个罪犯致敬或者团伙犯罪。
2013年1月20日 11:48 | # | 引用
冷知识 说：
神分析。。博士都这样？
2013年1月20日 19:27 | # | 引用
123 说：
且不说分析样本过小，我很好奇你为什么不先用这个方法分析我们的食品安全问题来说明我国在这方面是否恶化？我估计结论会和你这篇文章非常接近。
2013年1月21日 03:43 | # | 引用
awguo 说：
概率对应的平均多少周出现一次应该引用下算法嘛。不具体计算98%后面小数点的同学们都直接98/(1-98)得49了。跟59对比起来很像是typo
2013年1月28日 08:42 | # | 引用
爱国者 说：
文章作者把时间维度去掉了。
举个例子，
假如枪击事件发生的数量 按年份是这样的 5,4,3,2,1 ，显然枪击事件呈现下降的趋势；假如枪击事件发生的数量 按年份是这样的 1,2,3,4,5，那么枪击事件呈现上升的趋势。但根据文章作者的分析方法，两种情况下得出的结论是相同的。
文章要论证的是有没有恶化，是一个趋势，不能把时间维度去掉。
可能采用时间序列分析方法会比较合理些
2013年2月 3日 16:11 | # | 引用
鸟叔 说：
数量太少，是需要修订系数的，感觉这是大三学生做的推论，另外枪击事件真有那么少吗？应该考虑到持械案，而不是持枪致死。应该会得出截然不同的结果。
2013年2月 5日 11:15 | # | 引用
路过哈 说：
p-value 只有0.18。也就是说，对于"美国治安没有恶化"的结论，我们只有82%的把握，还有18%的可能是我们错了，美国治安实际上正在恶化。
还有这样解释的吗？那p-value是0.01，是不是说错的可能只有1%？
2013年2月18日 10:23 | # | 引用
wugr 说：
HI～我过几天打算买你翻译的那本《黑客与画家》。第一次看你那篇《互联网入门协议》时，我就发现，你写得深入浅出，是个真正做事的学者，今天又随便看了几篇文章，我觉得自己的判断没有错～
我喜欢关注这样的人，能增长知识并深受鼓励，我也会努力学习，做好自己的博客。真心祝你写出更多精彩的文章！
2013年2月19日 12:36 | # | 引用
pattision 说：
同样表示对p-value的解释存疑。数学功底不佳，不知p-value如何得来，真的代表文中所述含义吗？
2013年2月27日 17:20 | # | 引用
王子非 说：
中国如果不禁止枪支，看看，绝对比美国乱得多了，恐怕一个月的枪击案就比人家几十年还多。
2013年3月29日 11:08 | # | 引用
徐铭之 说：
请问枪击案那个，后面第三列的期望值怎么算出来的？虚心求教
2013年4月13日 23:02 | # | 引用
阿杜 说：
今天在看《统计推断》的内容，其中很多生活情景都可以用泊松分布来建模，上网搜一下泊松分布的其他应用，一搜就看到您的博文，泊松分布真的很强大
2013年4月24日 09:32 | # | 引用
fischerwang 说：
感觉应该更加符合幂律分布才对。
2013年4月27日 22:57 | # | 引用
么 说：
前年学的 全忘了
2013年5月17日 20:07 | # | 引用
maxime 说：
数据量太小，统计学基本原理基本都不适用
而且三个假设中只有第一个勉强过关，后两个明显是理想条件，我们先不说发生概率的问题，这个独立事件条件也不好满足，因为人类难免受到其他个体的影响，如果自始至终没有发生过这样的大规模枪击案，可能永远都不会有这样的事情发生，又或者米国颁布了禁止持枪法案，此类事件概率就更加微乎其微了
2013年10月 3日 16:47 | # | 引用
matteo 说：
98%概率不缺货时，应该是平均每50周发上一次缺货事件
2013年10月18日 19:33 | # | 引用
fedstyale 说：
p-value应该是我们拒绝假设，也就是如果我们说美国mass shooting均值升高的话，我们犯错的概率是18%，而正确的概率其实有82%，而不是接受假设正确的概率。相反，如果拒绝假设犯错概率越低，接受假设犯错概率概率越高。所以在文中，接受假设（mass shooting均值不变）犯错的概率其实是82%。所以p-value在0.9以上，接受假设犯错的概率才会比较低。这里具体是第一类错误和第二类错误的关系问题，文中把两者搞混。
2013年11月28日 18:01 | # | 引用
weiwang 说：
不知道有没有抄袭以下这篇文章：
http://www.wired.com/wiredscience/2012/12/are-mass-shootings-really-random-events-a-look-at-the-us-numbers/
2013年12月28日 10:07 | # | 引用
Leonhardt 说：
问一下 如果统计值与泊松分布有偏差，该怎么判断呢？
2014年3月23日 12:56 | # | 引用
张海鹏 说：
个人感觉概率统计理论对于现实社会的意义是提供了一个方向上的认识，比如说这篇文章谈到了是否美国治安环境在变坏？且不说这种方法在此前提下是严密还是不严密的，但是从统计学的角度看这个问题就是一个很不错的点儿，比如说MH370的寻找，前不久也有人说做Bayes推断啊等等之类的......
2014年6月 2日 19:45 | # | 引用
Susan 说：
看到过最简单清楚的
2014年11月10日 16:38 | # | 引用
newnewjiang 说：
最后一个表的第三列，泊松分布的期望值是怎么算出来的？
2015年8月20日 10:32 | # | 引用
辰采星 说：
博主的博文一向写得精美易懂，赞起来！
2015年12月 4日 20:51 | # | 引用
ken 说：
把Poisson分布每个k的概率算出，乘以所有枪击总数，得出来的就是每个k预测的值。
之后用chi square做是很合理的，我也本能地想到用chi square。
null hypo是数据遵从Poisson分布，alter hypo就是...恶化鸟。
2016年4月19日 18:55 | # | 引用
崔来希 说：
是什么意思还是不懂，代入 P｛X=0｝=e^(-2) 怎么算来的4.2，还请明示？
2017年1月 4日 23:02 | # | 引用
wysqh 说：
卡方检验里为什么自由度是7啊？
这里的自由度是怎么计算出来的。
2017年1月18日 16:39 | # | 引用
673556617 说：
准备补一下大学的概率论..
2017年2月 3日 05:39 | # | 引用
lh 说：
最后一个表的4.2和8.39怎么算的啊
2017年11月19日 17:56 | # | 引用
Monkee 说：
存货为4个罐头时，缺货发生的情况是每周卖出了5或6个罐头，概率为0.036+0.017=0.053；1周/0.053=18.86，所以约19周发生一次；
存货为5个罐头时，缺货发生的情况是每周卖出了6个罐头，概率为0.017；1周/0.017=58.82，所以约59周发生一次；
2018年2月17日 22:32 | # | 引用
SOPHIE80199 说：
统计学假设是两个样本H0 无差别。 p
2024年6月28日 22:19 | # | 引用
SOPHIE80199 说：
统计学假设是两个样本H0 无差别。 p
2024年6月28日 22:20 | # | 引用
SOPHIE80199 说：
不知道为什么，发不全留言。 博主对的。
2024年6月28日 22:20 | # | 引用