大多数人在高中,或者大学低年级,都上过一门课《线性代数》。这门课其实是教矩阵。

刚学的时候,还蛮简单的,矩阵加法就是相同位置的数字加一下。
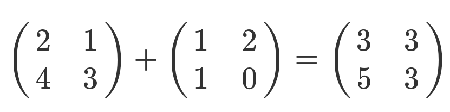
矩阵减法也类似。
矩阵乘以一个常数,就是所有位置都乘以这个数。
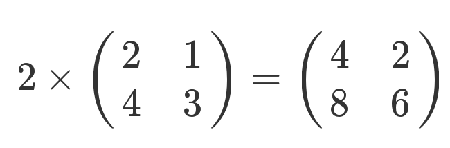
但是,等到矩阵乘以矩阵的时候,一切就不一样了。
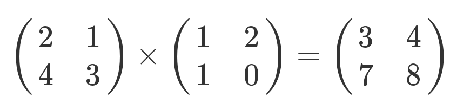
这个结果是怎么算出来的?
教科书告诉你,计算规则是,第一个矩阵第一行的每个数字(2和1),各自乘以第二个矩阵第一列对应位置的数字(1和1),然后将乘积相加( 2 x 1 + 1 x 1),得到结果矩阵左上角的那个值3。
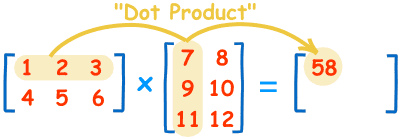
也就是说,结果矩阵第m行与第n列交叉位置的那个值,等于第一个矩阵第m行与第二个矩阵第n列,对应位置的每个值的乘积之和。
怎么会有这么奇怪的规则?
我一直没理解这个规则的含义,导致《线性代数》这门课就没学懂。研究生时发现,线性代数是向量计算的基础,很多重要的数学模型都要用到向量计算,所以我做不了复杂模型。这一直让我有点伤心。
前些日子,受到一篇文章的启发,我终于想通了,矩阵乘法到底是什么东西。关键就是一句话,矩阵的本质就是线性方程式,两者是一一对应关系。如果从线性方程式的角度,理解矩阵乘法就毫无难度。
下面是一组线性方程式。
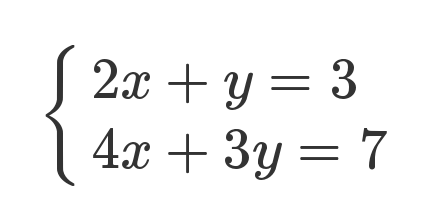
矩阵的最初目的,只是为线性方程组提供一个简写形式。
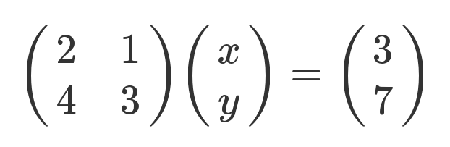
老实说,从上面这种写法,已经能看出矩阵乘法的规则了:系数矩阵第一行的2和1,各自与 x 和 y 的乘积之和,等于3。不过,这不算严格的证明,只是线性方程式转为矩阵的书写规则。
下面才是严格的证明。有三组未知数 x、y 和 t,其中 x 和 y 的关系如下。
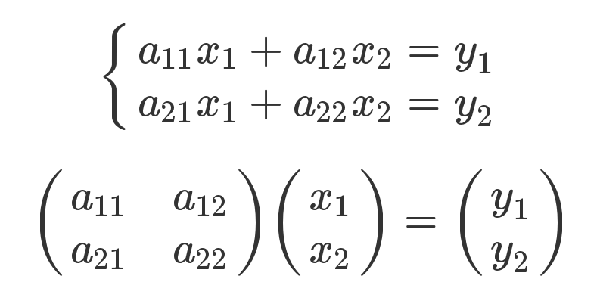
x 和 t 的关系如下。
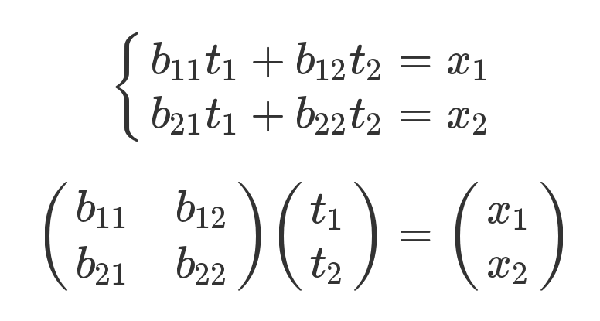
有了这两组方程式,就可以求 y 和 t 的关系。从矩阵来看,很显然,只要把第二个矩阵代入第一个矩阵即可。
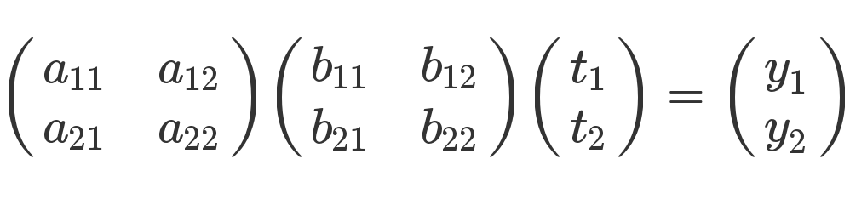
从方程式来看,也可以把第二个方程组代入第一个方程组。
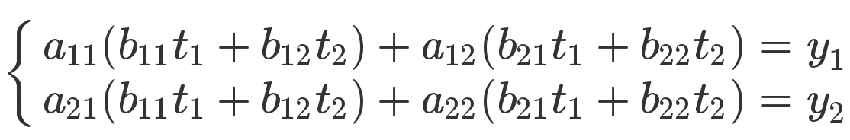
上面的方程组可以整理成下面的形式。
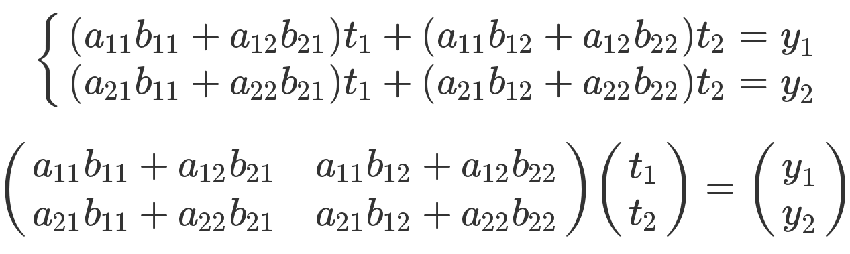
最后那个矩阵等式,与前面的矩阵等式一对照,就会得到下面的关系。
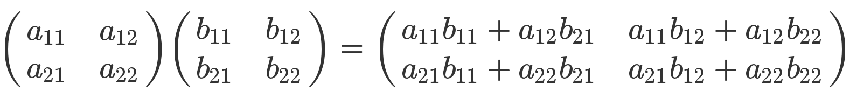
矩阵乘法的计算规则,从而得到证明。
=========================================
以下为广告部分。欢迎大家在我的网络日志投放广告。
[赞助商广告]
如果你想换工作,花五分钟,浏览一下 100offer,也许人生从此就会不同。
100offer 的目标是,只要你有2年以上的互联网工作经验(一线互联网公司更好),它就极有可能帮你拿到年薪 20W--80W 的 Offer。
它最近对514位用户的一份实证分析,有两点发现。
(1)所有离职的工程师之中,BAT员工最受欢迎,新工作的薪酬通常可以翻番。
(2)只有40%的程序员跳槽去了C轮、D轮和上市公司,其余60%都去了天使轮、A轮和B轮的公司,其中不乏资深的高级程序员。原因是这些创业公司刚刚起步、产品模式初步得到认可,上升空间大、技术人才需求量大、愿意给出较多的期权。

结合上面两点,年青程序员可以这样设计自己的职业生涯:
1、至少有一次大公司的成功工作经历。
所谓"成功",是指参与过知名的产品开发或主力项目经验。这一般代表你已经具备:良好的代码规范、团队协作能力、与大牛一起工作的开阔眼界成熟的技术体系。
2、然后,加入一家高速发展的创业公司。
100offer 帮助你实现这条职业道路。
(完)


你大爷 说:
这篇广告发的很硬啊·~~
2015年9月 1日 18:47 | # | 引用
uuspider 说:
阮老师是要开始研究算法了吗?
2015年9月 1日 18:57 | # | 引用
小恶魔 说:
@uuspider 高中基本知识而已,怎么能叫算法呢??
2015年9月 1日 19:11 | # | 引用
drunkevil 说:
这一点应该是理解矩阵乘法的基础,很多的线性代数书上面都有讲到,只是不一定每个老师都讲到,好多老师都把它作为选将部分,时间不够就不讲了。
2015年9月 1日 19:14 | # | 引用
swizard 说:
这个证明有问题吧? 从方程组到简写矩阵 这一步并没有证明。
2015年9月 1日 20:59 | # | 引用
NemoLuo 说:
这个以前Matric67有一篇文章, http://www.matrix67.com/blog/archives/4294 这里感觉更接近本质
2015年9月 1日 22:15 | # | 引用
lyapunov 说:
矩阵乘法是线性变换。在线性空间中,选定了基底的线性变换可以用矩阵乘法表示。通过研究矩阵,就可以研究对应的线性变换。比如,酉矩阵对应酉变换。
2015年9月 1日 23:10 | # | 引用
ChuckLu 说:
不太明白这个东西,你怎么现在才知道
矩阵的最初目的,只是为线性方程组提供一个简写形式。
你们用的是什么教材?我记得高中的时候,学习这个的时候。
书上很明确的提到了矩阵的目的,教材还是可以好好看看,逐字逐句
2015年9月 2日 08:30 | # | 引用
vingc 说:
残忍拒绝,这么残忍,会拉仇恨,为什么不改成“委婉拒绝”
2015年9月 2日 10:00 | # | 引用
quant67 说:
广告挺好的。
2015年9月 2日 12:33 | # | 引用
rt 说:
我们高中根本没这课,各个地方不一样的,别想当然
2015年9月 2日 17:40 | # | 引用
charles 说:
广告真遗憾,不是互联网的IT人可用不上。
2015年9月 3日 09:43 | # | 引用
jia 说:
我是学数学出身!!这些。。。。。1=1 1+1之类的
2015年9月 3日 14:19 | # | 引用
山下 说:
文字表达很清楚。
2015年9月 3日 14:34 | # | 引用
christopher 说:
本科的时候老师有提过。
2015年9月 3日 22:51 | # | 引用
uuspider 说:
矩阵运算是数组的应用,数组是算法和数据结构的基础,原文说"很多重要的数学模型都要用到向量计算,所以我做不了复杂模型",可见理解矩阵是为了做“复杂模型”,做模型一定是为了找到解决问题的方法,具体化到编程,就是算法。
2015年9月 4日 12:34 | # | 引用
蛀牙 说:
终于算是明白一二了。读书那会学矩阵、线性代数、复变函数这些课程,也是云里雾里。尤其复变函数,至今也是不明就里。阮博士应该去大学当老师才好。
2015年9月 5日 11:19 | # | 引用
weibo 说:
当时学的时候遇到乘法后就不理解了,为什么莫名其妙的来个这样的规则?我那博士老师的回答让我太失望了,就是这样的规则,他的思路一直在如何解上面跟我讲,我是想知道为毛有这规则。后来没办法,自己展开3位4位 ... 去发现规律,特么的隐约觉得这跟多项式有点关系?
但是这是什么规律啊,书上没一句说这个关系啊,网上也没有啊,课后习题也有跟多项式有关系的东西...老师上面讲的都是各种花哨的解体技巧,没兴趣,bug我自己也会找,但是就是不知道这个乘法规则到底跟解多项式是不是有一腿 ....
直到现在 ... 特么的 ... 简单的东西为毛包装的那么看起来很厉害的样子..
2015年9月 5日 11:29 | # | 引用
pood 说:
方老师能重新编辑下高等数学教材么?当年学微积分、线性代数和概率论,学得云里雾里的。
2015年9月 6日 13:33 | # | 引用
JazzCoder 说:
我就想不通为啥线代课本不能这样深入浅出的讲一下呢?
2015年9月 6日 14:02 | # | 引用
jqk6 说:
这篇文章在阮老师的博客出现感觉很突兀,阮老师是不是在指导自己的小孩学习数学呢?
2015年9月 6日 15:37 | # | 引用
藕黑~ 说:
记得孟岩也写过一个系列, 不过是很久很久以前的
2015年9月 7日 15:37 | # | 引用
Adrift 说:
JavaScript系列教程不错,非常感谢。
2015年9月 8日 09:54 | # | 引用
向死而生 说:
高中的时候教过的,但忘的差不多了。
2015年9月 8日 12:01 | # | 引用
fengchang 说:
孟岩的理解矩阵一二三,可惜只开了个头
http://blog.csdn.net/myan/article/details/647511
阮老师这次像是为了发广告挤出来一篇呀
2015年9月 8日 15:22 | # | 引用
zonxin 说:
数学运算/推导过程本身没有任何的意义,主要是看我们赋予它什么意义
2015年9月 9日 12:15 | # | 引用
程达 说:
矩阵方法能简化一些计算,但也有些很牛的数学家拒绝使用矩阵,认为矩阵无法理解。可见数学家也有自己的偏好和习惯的思维方式,跟智商无关。
我是在做图像处理时用过矩阵算法,感觉比较容易理解,容易转换成程序。其他方面从来没用过。
2015年9月10日 17:19 | # | 引用
DpR_Nino 说:
在方程组转换到矩阵方程的过程中,已经用到了矩阵方程的规则,等于是证明的过程中就用到了待证明的结论?
2015年9月10日 18:02 | # | 引用
JunkFood 说:
其实还是没说到线性组合
很多问题从线性组合的和线性空间的角度一下就清楚了
2015年9月12日 10:15 | # | 引用
Henry 说:
谁用过100offer啊,感觉这才是本文的重点吧
2015年9月13日 09:32 | # | 引用
zeallean 说:
khan 学院上有专门的一节课讲到这个。
2015年9月17日 15:55 | # | 引用
哈哈哈哈 说:
我还以为你用计算机程序说明这个计算过程,太失望了~~~
2015年9月18日 00:52 | # | 引用
uu 说:
建议不要只是自己想,找个国外的LA教程看下。这个理解还是有点浅薄。
2015年9月18日 09:14 | # | 引用
遗憾的猫 说:
以前我没学好数学,我就会说我数学老师死得早.现在看了你这文章后想想,他们真的早应该死掉去,特别是那些写教科书的人,那些就是死人啊死人死人.这么简单的东西被他们教得那么复杂难懂,只能说明他们的无知,跟没有学过的人一样的无知,无知,无知.
2015年9月27日 01:55 | # | 引用
tianpeng 说:
我刚刚写了一篇文章,希望对所有困惑于这个问题的人有帮助:
《再谈矩阵与矩阵乘法》
http://math.tianpeng.org/?p=1024
2015年10月 4日 01:01 | # | 引用
六日游生 说:
矩阵就是线性映射,每一个矩阵都有线性映射一一对应
矩阵乘法就是复合线性映射(f(f(x))。
复合映射也是一个线性映射,也就说也有对应矩阵
而矩阵乘法就是求出对应矩阵的方法公式
2015年10月 8日 10:40 | # | 引用
jiaru0123 说:
谢谢分享! 不过想请问一下。(如果不专业还请包含) 因为向量乘积也是定义空间中角度的方法。向请问,矩阵乘积与向量乘积在这个角度上又是怎样理解呢?
2015年10月23日 23:15 | # | 引用
xray 说:
这个证明没有问题的
2015年11月 2日 03:04 | # | 引用
caep121 说:
阮博士,看了你几篇余弦相似性的博客,讲得浅显易懂,让我这个没有基础的人一看就懂了。期待你能多讲一些,比如Jaccard、Dice等,非常感谢!
2015年11月 9日 16:31 | # | 引用
白水 说:
谢谢您精彩的解答,您后面的几个步骤也可以理解成为矩阵的乘法运算起源于函数的复合运算,即f(g(x)),这里带入矩阵即可。
2015年11月14日 18:44 | # | 引用
pc 说:
谢谢啊,我在上大学自己就是迷茫这个问题,感谢你的帮助非常感谢
2015年11月25日 19:16 | # | 引用
小妖 说:
我们高中可没教这个东西,现在终于明白了。 谢谢阮老师
2015年12月15日 15:41 | # | 引用
老司机 说:
广告设计的不错.
2016年2月17日 16:49 | # | 引用
太阳以北 说:
这个我们的线代老师提过,但没有您讲的那么详细。您让我对矩阵有了新的认识~
2016年5月 3日 19:13 | # | 引用
太阳以西 说:
把两个矩阵放在EXCEL里排排好,相交的行列就是你要计算的数据,每天处理数据就会发现矩阵乘法真是好东西,上学时怎么也理解不了
2016年5月25日 01:07 | # | 引用
黄桢桂 说:
有矩阵除法吗,怎么算,求解答,谢谢!
2016年6月14日 11:10 | # | 引用
zz1058 说:
看完这篇,没懂矩阵存在的意义,让人感觉只是为了书写形式而书写的一种存在。还有个问题是,因为你已经脑袋里面是已经知道矩阵乘法规则是要这样写,你的证明为什么我觉得是为了拼凑规则。
上面有个同学说:从方程组到简写矩阵 这一步并没有证明。同感。
2016年6月25日 19:04 | # | 引用
dd 说:
我看完原文,感觉这句话最重要:
The reason why this works is that matrix multiplication was designed so that if you multiply a matrix by the vector with all zeroes except a 1 in the i-th entry,then the result is just the i-th column of the matrix.
自己翻译一下:矩阵乘设计目标是:一个向量(只有一个1)乘以一个矩阵,假设1是第i个元素,那么乘积结果是矩阵第i列存在,其他都是0.
这里向量是空间是(0,0,1,0)这样的形式。
所以才有了行列乘积和的矩阵计算方式。
正因为如此,结合线性function特点,后面才有:
f(g(w1))=f(w1+w2)=f(w1)+f(w2)=(2w1+4w2)+(w1+3w2)=3w1+7w2,...
从而映证了乘积和是矩阵乘计算规则。
到这里矩阵乘计算规则可以接受了。
2016年6月30日 15:06 | # | 引用
www 说:
我认为,应该从回答乘法的本质说起,乘法的本质就是复合映射,比如说,数是什么,是计数,人们最早对数的认识,如3个苹果,3个梨子,但是3×3你不能说是三个苹果乘以三个苹果结果是什么9个苹果的平方吗?不是,应该这么理解三个篮子,一个篮子里有三个苹果,他们的乘积就是九个苹果,第一个三可以理解为线性代数的恒等映射即三个苹果,第二个三指的是三篮子什么,两者相乘,就是复合映射即三篮子苹果的概念,读点数学史还是有帮助的
2016年7月 5日 14:57 | # | 引用
三五 说:
觉得证明还是有点问题的,用到的方程组用矩阵的方式表示不就是默认了矩阵的乘法吗?还是我有点混淆?
2016年7月19日 08:59 | # | 引用
Jocelyn 说:
醍醐灌顶,如果大学的时候就关注阮老师 说不准真能学好线代。
2016年7月22日 16:19 | # | 引用
随你 说:
我读计算机系的时候,听说数学很重要,就把高等数学,线性代数,离散数学,概率等这些科目都学得很好,一般每一科都在90分以上,特别是线性代数,竟然能考到106分,总分为110分。可出来学的这些知识一点都没用上。
2016年8月 9日 23:23 | # | 引用
cymurs 说:
但是,它却是理解矩阵乘法的关键。不理解的东西,学起来就会没动力。老师往往缺少这样的实践
2016年9月 1日 15:19 | # | 引用
xesam 说:
因为你看错了书,国外的翻译教材基本都是这么讲的。。。
2016年9月 5日 21:54 | # | 引用
程序猿 说:
大学老师要是这么讲!我就早!明!白!了!好么,这个应该放在矩阵课本第一页
2016年9月26日 12:21 | # | 引用
@ 说:
我觉得矩阵乘法不需要证明,它就是人设定的规则,就要那么写,又不是自然规律
2016年10月 6日 14:01 | # | 引用
雩而雨 说:
作为刚接触数组的编程小白,这篇文章解了我的惑,易懂。
2016年10月10日 16:50 | # | 引用
攻城狮 说:
通俗易懂,又回顾了一下矩阵算法,谢谢。
2016年10月14日 13:12 | # | 引用
hellow 说:
其实是这样的:
矩阵*向量 可以看作空间转换后的线性组合。
2017年1月18日 23:22 | # | 引用
kami 说:
把开头的0112换成0123其实更好懂点 不过看到后面也明白了 谢谢老师 很有帮助
2017年2月 7日 16:02 | # | 引用
学习者 说:
可否展开具体说说呢?多谢
2017年2月16日 13:49 | # | 引用
donghua 说:
这个证明真是扯啊,仔细看步骤,中间有一步是用矩阵的乘法规则去展开矩阵,然后比照得出结论,这是用结论证明结论。
矩阵的乘法是一种定义,不需要证明的啊,同时也是无法证明的啊,是一个概念。类似的其他规则的乘法有逐项乘,数乘,还有哈达玛矩阵乘法,都是历史时期数学家为了解决某些问题引进的规则。为什么通常意义的矩阵乘法是这样?这个楼上有人说了是最初为了解多元一次方程组引入的。
我看不少人看完之后纷纷觉得醍醐灌顶,然后咒骂数学老师没讲明白,突然觉得我们中国的工程师的数学素质好差啊。
2017年4月27日 17:07 | # | 引用
Tony 说:
你没混淆,博主就是在扯淡。哪有用结论去证结论的。建议楼主改改。不要再让一些“程序猿”觉得恍然大悟之后,再让自己的数学老师背锅了。
2017年4月27日 17:10 | # | 引用
robin xu 说:
确实,虽然矩阵乘法我之前也没明白原理,但看中间的证明过程有一步感觉就是用结论证明结论。。
2017年4月29日 23:56 | # | 引用
ps 说:
1、矩阵乘法是定义;2、证明却有已知p,求证p味道
2017年6月10日 15:58 | # | 引用
shaka 说:
我一开始也是以为用结论证明结论。只因为“从方程式来看,也可以把第二个方程组代入第一个方程组。”这一步没真正搞清楚。
2017年7月 3日 12:27 | # | 引用
小浩 说:
B站里有3blue1brown,线性代数的本质,里面讲得很有意思。
2017年7月19日 20:28 | # | 引用
xiaoxiao 说:
这是错误的证明方式,你先用了矩阵相乘的规则,然后去证明矩阵相乘具有这样的规律。就向上所说的1 = 1,使用了1 = 1这个规则去证明1 = 1,这是不成立的。
2017年8月 5日 11:00 | # | 引用
zhangxiaoping 说:
楼主把自己绕进去了。这算什么证明?假如我改一下"矩阵乘法规则",比如是将两个乘积相减,然后用你的方法,也能证明出相减的规则是正确的。
哈哈哈哈哈啊哈哈哈!
2017年8月20日 11:17 | # | 引用
简扬 说:
阮老师,我觉得知乎这个回答讲的很不错,算是讲了一个简单的模型:
https://www.zhihu.com/question/21351965
2017年9月 1日 10:09 | # | 引用
王宁 说:
能把复杂的东西说清楚,就非常的不容易。厉害!!!
2017年9月 5日 11:09 | # | 引用
吴纨绔 说:
第二个矩阵代入第一个矩阵那一步所得等式用了矩阵结合律,(a11,a12,a21,a22)(x1,x2)=(a11,a12,a21,a22)(b11,b12,b21,b22)(t1,t2)不对,(a11,a12,a21,a22)(x1,x2)=(a11,a12,a21,a22)[(b11,b12,b21,b22)(t1,t2)],结合律没有证明不能使用。
2017年9月15日 15:58 | # | 引用
tpig 说:
还是应该看英文原版,感谢提供链接。
https://nolaymanleftbehind.wordpress.com/2011/07/10/linear-algebra-what-matrices-actually-are/
2017年9月19日 12:30 | # | 引用
关中刀客 说:
看阮老师这个过程一目了然!
当年在大学接触的矩阵运算,没有这些证明过程,光死学法则,也看不到应用场景,导致我厌学,貌似还挂了┭┮﹏┭┮
2017年10月 6日 10:39 | # | 引用
贾海瑞 说:
哇,,还好我是初学就看到这个,太赞了,一直想不通行列式跟矩阵到底是干啥的来着
2017年10月12日 21:37 | # | 引用
TsaoLee 说:
正如阮老师开篇说的,对于矩阵乘法我一直也处于云里雾里的状态,今天有幸看到此文,顿时拨开了我心头迷雾,大赞
2017年11月 6日 23:42 | # | 引用
p 说:
3X3…矩阵没证明
2017年11月 8日 23:34 | # | 引用
子凡 说:
这广告发的,朴实无华,有理有据,是年青程序猿的不二算泽
2018年1月 8日 18:37 | # | 引用
Jackie 说:
最后这个证明怎么好象是用矩阵相乘的公式证明矩阵相乘公式?因为最后一步整理成 t1\t2 这一步貌似就用了公式啊
2018年3月13日 11:36 | # | 引用
12333334 说:
这个可以说是一种理解方式,但并不是矩阵相乘定义的历史真相或者最初发现,因为在把线性方程组写成矩阵形式Ax=b的时候已经包含了矩阵的乘法规则:对应行元素于对应列元素点乘然后相加。发展过程应该是人们在求解线性方程组时,发现”某种表达“可以简化求解符号,然后“某种表达”成了矩阵,再后来发现了利用矩阵本身还有更多优良性质。。。。。。。
2018年7月16日 21:03 | # | 引用
user 说:
x1,x2, t1,t2竖着写,就是莫名的看不惯,横着写也一样可以证明啊
2018年11月28日 17:51 | # | 引用
啦啦啦 说:
博主可能不是想当然,可能是记错了,我们高中没用这个路子教,大学用了这个路子。当然也可能像你说的,有的地方高中就这么教了有的没有
2018年12月 1日 01:21 | # | 引用
啦啦啦 说:
对我来说蛮合用的,我就想把忘了的乘法简单计算唤醒个记忆,这篇帮我目的达成。我上课老师也是走这个路子的,路子一样所以恢复记忆更快了。适合我
2018年12月 1日 01:26 | # | 引用
钟 说:
矩阵相乘的本质无非就是空间的基向量的变换。
2019年5月11日 09:27 | # | 引用
aaron 说:
这个矩阵必须是正方形才成立吧?
如果是d-dimension * (n-dimension*d-dimension),其中,d<>n,您这个还能证明?
2020年3月 8日 22:13 | # | 引用
王一波 说:
书上就是这么介绍的,你不懂肯定是书没学好
2020年4月19日 09:28 | # | 引用
青云 说:
同感,感觉还是用矩阵乘法的规则去证明矩阵乘法的规律
2021年1月22日 14:31 | # | 引用
教育不良 说:
你高中就学矩阵了?
2021年3月25日 10:47 | # | 引用
辛烜 说:
非常感谢,一下就理解了
2021年4月 2日 14:27 | # | 引用
zzy2357 说:
这个网站不错,以动画的形式演示矩阵相乘的过程
http://matrixmultiplication.xyz/
2021年8月29日 22:11 | # | 引用
王丙谦 说:
翻了10站,看不懂。这站看懂了,忒好。
2021年10月26日 19:07 | # | 引用
Charles Zhu 说:
https://www.mathsisfun.com/algebra/matrix-multiplying.html
这个链接就有点乘的基础教学。
2022年4月17日 15:02 | # | 引用