布尔代数是计算机的基础。没有它，就不会有计算机。
布尔代数发展到今天，已经非常抽象，但是它的核心思想很简单。本文帮助你理解布尔代数，以及为什么它促成了计算机的诞生。
我依据的是《编码的奥妙》的第十章。这是一本好书，强烈推荐。
一、数理逻辑的起源
19世纪早期，英国数学家乔治·布尔（George Boole，1815－1864）突发奇想：人的思想能不能用数学表达？
此前，数学只用于计算，没有人意识到，数学还能表达人的逻辑思维。
两千年来，哲学书都是用文字写的。比如，最著名的三段论：
所有人都是要死的，
苏格拉底是人，
所以，苏格拉底是要死的。
乔治·布尔认为，这种推理可以用数学表达，也就是说，哲学书完全可以用数学写。这就是数理逻辑的起源。
二、集合论
乔治·布尔发明的工具，叫做"集合论"（Set theory）。他认为，逻辑思维的基础是一个个集合（Set），每一个命题表达的都是集合之间的关系。
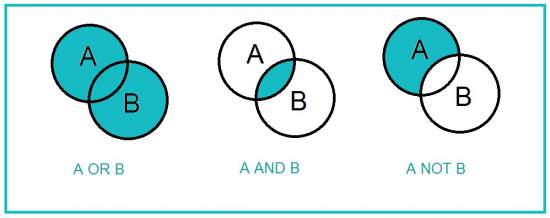
比如，所有人类组成一个集合R，所有会死的东西组成一个集合D。
所有人都是要死的
集合论的写法就是：
R X D = R
集合之间最基本的关系是并集和交集。乘号（X）表示交集，加号（+）表示并集。上面这个式子的意思是，R与D的交集就是R。
同样的，苏格拉底也是一个集合S，这个集合里面只有苏格拉底一个成员。
苏格拉底是人
// 等同于
S X R = S
上面式子的意思是，苏格拉底与人类的交集，就是苏格拉底。
将第一个式子代入第二个式子，就得到了结论。
S X (R X D)
= (S X R) X D
= S X D
= S
这个式子的意思是，苏格拉底与会死的东西的交集，就是苏格拉底，即苏格拉底也属于会死的东西。
三、集合的运算法则
前面的三段论比较容易，一眼就能看出结论。但是，有些三段轮比较复杂，不容易立即反应过来。
请看下面这两句话。
"鸭嘴兽是卵生的哺乳动物。鸭嘴兽是澳洲的动物。"
你能一眼得到结论吗？
鸭嘴兽 X 卵生 = 鸭嘴兽
鸭嘴兽 x 澳洲 = 鸭嘴兽
将第一个式子代入第二个，就会得到：
鸭嘴兽 X 卵生 x 澳洲 = 鸭嘴兽
// 相当于
卵生 x 澳洲 = 鸭嘴兽 + 其他
因此，结论就是"有的卵生动物是澳洲的动物"，或者"有的澳洲的动物是卵生动物"。
还有更不直观的三段论。
"哲学家都是有逻辑头脑的，一个没有逻辑头脑的人总是很顽固。"
请问结论是什么？
这道题会用到新的概念：全集和空集。集合A和所有不属于它的元素（记作-A）构成全集（I），这时A和-A的交集就是一个空集（0）。
A + (-A) = I
A X (-A) = 0
因此，有下面的公式。
B
= B X I
= B X (A + -A)
= B X A + B X (-A)
回到上面那道题。
哲学家 X 逻辑 = 哲学家
无逻辑 X 顽固 = 无逻辑
根据第一个命题，可以得到下面的结论。
哲学家 X 无逻辑
= (哲学家 X 逻辑) X 无逻辑
= 哲学家 X (逻辑 X 无逻辑)
= 哲学家 X 0
= 0
即哲学家与没有逻辑的人的交集，是一个空集。
根据第二个命题，可以得到下面的结论。
无逻辑 X 顽固
= 无逻辑 X 顽固 X (哲学家 + 非哲学家)
= 无逻辑 X 顽固 X 哲学家 + 无逻辑 X 顽固 X 非哲学家
= 0 X 顽固 + 无逻辑 X 顽固 X 非哲学家
= 无逻辑 X 顽固 X 非哲学家
= 无逻辑
也就是说，最终的结论如下。
无逻辑 X 顽固 X 非哲学家 = 无逻辑
// 相当于
顽固 X 非哲学家 = 无逻辑 + 其他
结论就是顽固的人与非哲学家之间有交集。通俗的表达就是：一些顽固的人，不是哲学家，或者一些不是哲学家的人，很顽固。
由此可见，集合论可以帮助我们得到直觉无法得到的结论，保证推理过程正确，比文字推导更可靠。
四、 集合论到布尔代数
既然命题可以用集合论表达，那么逻辑推导无非就是一系列集合运算。
由于集合运算的结果还是集合，那么通过判断个体是否属于指定集合，就可以计算命题的真伪。
一名顾客走进宠物店，对店员说："我想要一只公猫，白色或黄色均可；或者一只母猫，除了白色，其他颜色均可；或者只要是黑猫，我也要。"
这名顾客的要求用集合论表达，就是下面的式子。
公猫 X (白色 + 黄色)
+ 母猫 X 非白色
+ 黑猫
店员拿出一只灰色的公猫，请问是否满足要求？
布尔代数规定，个体属于某个集合用1表示，不属于就用0表示。 灰色的公猫属于公猫集合，就是1，不属于白色集合，就是0。
上面的表达式变成下面这样。
1 X (0 + 0)
+ 0 X 1
+ 0
= 0
因此，就得到结论，灰色的公猫不满足要求。
这就是布尔代数：计算命题真伪的数学方法。
五、布尔代数的运算法则
布尔代数的运算法则与集合论很像。
交集的运算法则如下。
1 X 1 = 1
1 X 0 = 0
0 X 0 = 0
并集的运算法则如下。
1 + 1 = 1
1 + 0 = 1
0 + 0 = 0
集合论可以描述逻辑推理过程，布尔代数可以判断某个命题是否符合这个过程。人类的推理和判断，因此就变成了数学运算。
20世纪初，英国科学家香农指出，布尔代数可以用来描述电路，或者说，电路可以模拟布尔代数。于是，人类的推理和判断，就可以用电路实现了。这就是计算机的实现基础。
六、布尔代数的局限
虽然布尔代数可以判断命题真伪，但是无法取代人类的理性思维。原因是它有一个局限。
它必须依据一个或几个已经明确知道真伪的命题，才能做出判断。比如，只有知道"所有人都会死"这个命题是真的，才能得出结论"苏格拉底会死"。
布尔代数只能保证推理过程正确，无法保证推理所依据的前提是否正确。如果前提是错的，正确的推理也会得到错误的结果。而前提的真伪要由科学实验和观察来决定，布尔代数无能为力。
（完）
mark 说：
好烧脑子~
2016年8月 5日 09:01 | # | 引用
Kevin 说：
鸭嘴兽 X 卵生 x 澳洲 = 鸭嘴兽
// 相当于
卵生 x 澳洲 = 鸭嘴兽 + 其他
这就没有弄明白
2016年8月 5日 09:04 | # | 引用
Kevin 说：
鸭嘴兽那个推导没看懂
2016年8月 5日 09:20 | # | 引用
vook 说：
不是吧 这都是基础啊 离散数学
2016年8月 5日 09:21 | # | 引用
hjk0820 说：
布尔代数的运算法则看得直观
2016年8月 5日 10:06 | # | 引用
yingshin 说：
绕的好晕~有三段轮的笔误
2016年8月 5日 10:37 | # | 引用
zskm 说：
鸭嘴兽和卵生*澳洲的交集是鸭嘴兽，说明鸭嘴兽是卵生*澳洲的子集，也就是一部分，那么卵生*澳洲所构成的集合就包含鸭嘴兽，可能包含其他元素也可能不包含
2016年8月 5日 12:01 | # | 引用
MGhostSoft 说：
S X (R X D)
= (S X R) X D
= S X D
= S
最后一步 S X D = S 是怎么得出来的？
2016年8月 5日 13:43 | # | 引用
fyzzy 说：
无逻辑 X 顽固 X 非哲学家
= 无逻辑
这里是怎么推导的呢？
2016年8月 5日 15:31 | # | 引用
safarishi 说：
有的地方看得就像是绕口令一样：
像：
"哲学家都是有逻辑头脑的，一个没有逻辑头脑的人总是很顽固。"
不过让我觉得数学真的很厉害，只可惜以前没有好好学，不开心
2016年8月 5日 21:08 | # | 引用
胡子拉碴 说：
最后一段也就是说布尔代数不产生新知识
2016年8月 6日 10:22 | # | 引用
gzq 说：
文章很棒，顺便说下，数理逻辑的起源部分第一句“18世纪早期”应该是“19世纪早期”。
2016年8月 6日 18:28 | # | 引用
warrenLOL 说：
推荐去Coursera上Duke大学Walter Sinnott-Armstrong教授所教的Think Again: How to Reason and Argue,非常非常好的逻辑课程，这篇博文中的内容都有所涵盖。
2016年8月 8日 09:36 | # | 引用
Jim_Chen 说：
不知道是不是我记错了：
1. 在我认知中，集合论的创立与布尔没有直接关系，而关系最紧密的是后来之人康托尔
2. 在集合运算中并，交都有特定的符号：∪和∩，而×，＋在集合中又有其他具体含义，×代表笛卡尔积，而＋是集合的计数原理也就是容斥定理中引入的，举个栗子就是假定A与B都是有限集合，那么A+B=(A∪B)+(A∩B)
3. 其实我觉得布尔运算是命题逻辑的基础，但是纯粹的命题逻辑不能解决上述的很多例子，因为部分例子涉及了谓词逻辑，必须引入两个谓词，全称和存在才能解决，这也是命题逻辑的缺陷，比如著名三段论就是纯粹用命题逻辑无法解决的问题。而我感觉博主一直只用命题逻辑的范围解决问题感觉困惑。
2016年8月 9日 01:59 | # | 引用
Don 说：
编码的奥妙 ---> 编码的奥秘
2016年8月 9日 18:18 | # | 引用
leyunu2010 说：
这篇写的一般。
《编码》里讲的更清楚。Charles Petzold的那本。
2016年8月10日 15:28 | # | 引用
linxianqing 说：
讲的太好了,浅显易懂,我老师要是教的这么好就好了
2016年8月12日 14:00 | # | 引用
Cindy_1 说：
这不就是数字电路的基础？
2016年8月16日 18:20 | # | 引用
eddie 说：
哇塞，不错
2016年8月17日 17:54 | # | 引用
lili 说：
并集的运算法则如下。
1 + 1 = 1
1 + 0 = 1
0 + 0 = 0
应该是1+1=2.
2016年8月29日 14:40 | # | 引用
raven 说：
这不是数学运算法则，是并集
2016年8月29日 18:10 | # | 引用
dolomite 说：
我也看不懂这个，希望有大神可以给解答一下
2016年9月 4日 01:25 | # | 引用
张中华 说：
2016年9月12日 10:22 | # | 引用
K 说：
前面不怎么烧脑子主要就是文字讲的有点绕 然后就是哲学家那里比较烧点脑子 其他的没什么
2016年9月15日 16:05 | # | 引用
wuiwe 说：
我寫一點我的簡單看法(本人化學混畢業的) (以下都沒查證，都是個人感覺)
1. 那圖叫做文氏圖，不叫做集合論 (理解文氏圖不代表理解集合論)
2. 我不覺得布爾代數是什麼創新 (我認為"方便"上創新，本質上沒創新)
其次 (and or 等等不叫做集合論，那叫做常識)
文氏圖的交集等等不是根本 (源頭)
3.源頭是什麼? (假設是二元邏輯)
真值表，就是二元邏輯，然後文氏圖的根本不是交集 (多數人只會照著書本想)
(雅里士多德的三段論)什麼是 if a than b (很醜陋的
然後就蹦出一個二元邏輯的真值表?
其實是一個大圓，裡面畫一個小圓，很明顯有3個區域，代表3個 True
真值表4個情形，只有一個Flase，正好是代表不存在
3個 True代表存在，這個類比可以聯想到機率論的樣本空間。 (細節我不描述了，大家都懂，樣本空間的意義很簡單，可是也能很深刻。)
我覺得這種基於空間的類比，比電路圖更適合類比布爾邏輯
(但是布爾邏輯和電路圖比文氏圖好用、好運算)
量子力學底層很多常見邏輯運算與日常不同，如何給出一個簡單的類比呢?
很簡單，一個文氏圖，如果是邏輯的類比，那麼如果縮的足夠小，顯然我們一開始憑藉的大小範疇關係已經失去效用了，顯然微小的事物沒必要遵循我們所謂的邏輯。
(弗雷格算數什麼的，我覺得很醜的，比"三段論"這爛名字還醜)
計算機用布爾代數來描述底層電路我認為確實是最好的選擇，不用浪費時間搞"哲學"
2016年9月20日 07:30 | # | 引用
wui 说：
有人可能會覺得我講這幹嘛?
因為我從小就覺得什麼
蘇格拉底是人，什麼人都會死，這根本沒資格稱為邏輯。(因為我們其實是靠日常經驗在空想)
那些傻孩子說什麼對對對，我理解了。
請問你看過死人? 請問你看到所有活著的人，都死了嗎?
我舉的類比(以前人早就發明)，是真正的邏輯實驗 (簡單的邏輯=範疇，其他邏輯系統不討論)
1. b包含a 直接導出 if a than b，直接等價於真值表
2. If 你落在a 廢話一定落在b。 自己拿筆戳一戳，全世界誰敢質疑這實驗?
當然用電路來模擬邏輯，可以"實現"邏輯，但是任何人都會問，憑什麼邏輯會在語言、電路上起作用呢?
所以說以為理解電路實現，或者什麼蘇格拉底死不死，或者舉出一堆語言上的日常類比，其實(我認為)都不算理解中學程度的邏輯，只是死背。
2016年9月20日 07:41 | # | 引用
wuiwe 说：
我覺得很多書籍扯一堆，然後有些傻孩子還是不理解(不接受)真值表，(因為他們不想死背)其實滿可愛的，話說我大學的數學教授(德國博士)也不理解真值表。(的簡單正確類比)
所以如果以德國數學博士的標準來看那些長篇大論，扯東扯西的書籍，也不能說那些作者都是犯傻。
(我以上說的理解都是指合情的接受，不是說真懂，世界上真懂得幾隻手指數得出來，但是不懂一樣可以過生活的。)
2016年9月20日 07:49 | # | 引用
wui 说：
1. 你沒記錯，但是康托爾偉大是更深層的，
布爾類似於把雅里士多德的三段論講得更清楚，搞一套數理邏輯的"符號規則"那樣。 (我感覺)
2. 我認為(不談那種哲學書扯一堆術語)直接說大部分談到三段論的書籍，亂扯的日常例子，本質上都是胡扯，都有漏洞。
而哲學家很愛基於語言去探討，扯出一大套術語，然後還要研究語言怎麼用如何，什麼xx詞，全稱，.......。
(目的只是要探討怎樣說話才合(他們的)邏輯，但是我們又沒有要寫哲學論文，去看一堆術語做什麼呢?)
在我看來，直接把那一堆例子丟到垃圾桶，告訴小朋友們基於科學實驗，
基於電路實驗，基於(我前面舉出的例子)你拿筆戳一個大小範疇，邏輯是對的。
(邏輯足以描述這2個實驗)
錯的是你亂套邏輯，而那些號稱很有邏輯的邏輯書(特別是哲學系、文學系寫的)，通常都是在亂套。
2016年9月20日 08:09 | # | 引用
wuiwe 说：
不談哲學的好處(因為我不懂)，我認為哲學的遺毒可以輕易的消除。
1. 只要問崇拜哲學的人，請問雅里士多德的時候哲學是物理還是數學還是語義學等等?
2. 請問哲學家搞得出相對論、量子力學嗎?
他們會直接得到2個結論(當然是憑感覺)
1. 當一個東西不能扯的時候(足夠清晰)他就脫離了哲學，所以哲學家有一部分整天在扯。
2. 哲學家很少深刻的影響世界
我沒有要貶低(經濟、數學、物理、政治、........)-哲學家
我鄙視哲學-哲學家
2016年9月20日 08:37 | # | 引用
Ray 说：
非常感谢您的blog！解答了很多我的问题！感谢！
2016年10月 9日 19:24 | # | 引用
刀刀 说：
苏格拉底 S D R那个推断过程是错的，正确的应该是：
已知： S X R = S (苏格拉底是人） R X D = R （人都会死）
要证明：S X D = S（苏格拉底会死）
过程是： S X D = (S X R) X D = S X (R X D) = S X R = S
2016年12月12日 17:15 | # | 引用
卡卡 说：
谢谢阮一峰大大！学了不少东西。
2016年12月19日 10:24 | # | 引用
超哥哥 说：
可以讲讲布尔代数的局限，以及后来的二阶逻辑。
2016年12月31日 14:55 | # | 引用
wuiwe 说：
這種東西很簡單，你懂一開始的直覺後面都顯然，只是運算符號誰優越，至於哲學上的討論那是很麻煩的。
我跟你講很多人就是被符號跟語言侷限，然後才會後面動不動卡住。就像是 calculus 一開始你懂這個極限語言的好處（可能要看一下數學史），然後你有直觀很好，但是後面是抽象符號更好用，直觀只是輔助，理論上來說邏輯很多都是規則套來套去，你懂最前面1頁全懂，半本書一定懂，至於後半本到了後期的研究什麼的不懂不會怎樣，數學系不懂的人也有，哲學系很懂但是只會玩玩符號的人懂了沒啥意義。
最根本的問題就一句話，邏輯為何對現實有用，這是哲學問題，數理邏輯上的討論系統自洽之類的，並不是這種哲學問題。
而很多動不動一套哲學的低階邏輯滿天飛得，我看到過一個數學家的名言，如果你的內容很貧乏，就把他用一階邏輯來寫。
像是很多人新手發問，他們只會背課本，聽說中國的中學就上什麼，逆命題、否命題、否逆命題等等。
很多人跟著課本死套，跟著這種可笑的符號系統，拜託數理邏輯老早有更適合人腦的符號系統了，一堆人用一堆術語在嚇人。
我舉的例子，有些人只看到表面，事實上這麼這麼簡單的文氏圖，對這些規則來說都是成立的，什麼迪摩根定律，什麼 for all, there exist，什麼否逆命題成不成立，不用動腦，例如 if a then b 成立，那麼這個邏輯圖像， if -a then -b，你戳非a跟非b外面，有沒有這個樣本空間？ 存在啊，而且我不是傻傻的套，我知道這個在事件跟機率上的意義，你具體的事情如何套都只是單一事件，沒有圖像讓人有側面的理解，也沒點到機率的意義，那很多哲學騙錢書整天扯淡蘇格拉底死不死就是超級笑話。
數理邏輯簡單講，一開始你接受，你有直覺類比，或者你笨笨的用語言套套套死記規則，反正你只要願意接受前面規則的有效性，半本書都可以看懂，後面半本已經是常人不需要理解的東西了，不是太無趣就是太機械，很多公理是邏輯學家搞的，正常人能把整本書的定理都證明完畢就謝天謝地，管底層的公理是好高騖遠。
2017年2月24日 22:39 | # | 引用
mcfly555 说：
@wui：
哲学家把简单的事实搞的特别复杂，物理世界的特性被人利用。不过数学化的理论发明先于物理世界的发现罢了。当物理世界有了发现，人总是是要上升到理论层面，为了便于人类控制。如果非要说哲学，我倒是凭借有限的经验觉得思维和存在是有同一性的，但是思维的局限在于仅仅是抽象，抽象出各种关系，即所谓的规律，对感知真实没有丝毫作用，换句话说思维只能模拟关系，是模拟而非真实。哲学在这里就显得很无聊，闲的蛋疼。维特根斯坦确实是过去那种弯弯绕绕的哲学的终结，海德格尔存在主义也更加真实有意义。粗人一个，哲学家说的再多也抵不上直接干，就是干。
2017年7月31日 18:52 | # | 引用
mzxc 说：
人都会死 X 死 = 人
2017年9月 5日 17:11 | # | 引用
hashkey 说：
无逻辑 X 顽固 X 非哲学家
= 无逻辑 X 顽固 X (I - 哲学家)
= 无逻辑 X 顽固 - 无逻辑 X 哲学家 X 顽固
= 无逻辑 X 顽固 - 0
= 无逻辑 X 顽固
= 无逻辑
2017年11月23日 14:09 | # | 引用
hashkey 说：
楼上刀刀的正解
S X D = (S X R) X D = S X (R X D) = S X R = S
2017年11月23日 14:12 | # | 引用
简单 说：
苏格拉底的人 x 人类 x 会死的东西
S X R X D
其实不用交换，最底层的交集永远都是S，只是作者上面的例子 S跟R 更有关系，所有将S与R括在一起。
2018年4月 8日 15:10 | # | 引用
雁南飞 说：
这个可以去看 李永乐老师讲的 数字电路与模拟电路那课，讲的非常清晰！！！！
2018年8月21日 15:30 | # | 引用
dawningblue 说：
逻辑能保证程序正义，而不能保证结果正义
如同科学思维能够保证过程是正确的，而不能保证结论是正确的
2019年5月31日 16:20 | # | 引用
牛继陆 说：
读了几遍。真好。
2020年11月11日 11:45 | # | 引用
lee20 说：
数学家布尔的后代与中国还有很多因缘呢
2021年6月11日 16:24 | # | 引用
大二学生 说：
为什么说“布尔发明的工具，叫集合论”，我查阅到的资料里，德国数学家康托尔（Georg Cantor）是集合论的创立者。
2023年9月16日 08:59 | # | 引用
天冬 说：
这里通过多个限制性定语来定义“鸭嘴兽”这一概念，但这种限定可能是必要不充分的，逻辑上同时满足“卵生”“澳洲动物”“哺乳动物”的未必只有鸭嘴兽。“鸭嘴兽 X 卵生 x 澳洲 = 鸭嘴兽”的意思就是“鸭嘴兽”存在于“卵生 x 澳洲”的集合中（因为“鸭嘴兽”与它的交集不是空集，而且就是“鸭嘴兽”自身）表述了“存在性”；“卵生 x 澳洲 = 鸭嘴兽 + 其他”也是一样的意思，只是“存在性”定义，而不是“唯一性”定义。
2024年10月27日 10:16 | # | 引用