统计学里面,正态分布(normal distribution)最常见。男女身高、寿命、血压、考试成绩、测量误差等等,都属于正态分布。
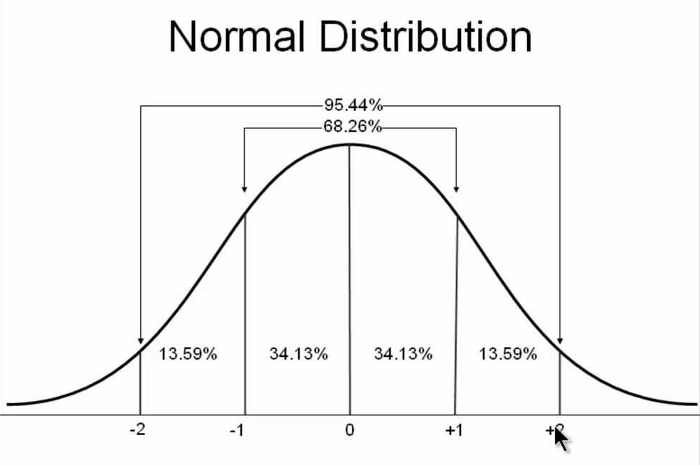
以前,我认为中间状态是事物的常态,过高和过低都属于少数,这导致了正态分布的普遍性。最近,读到了 John D. Cook 的文章,才知道我的这种想法是错的。
正态分布为什么常见?真正原因是中心极限定理(central limit theorem)。
"多个独立统计量的和的平均值,符合正态分布。"
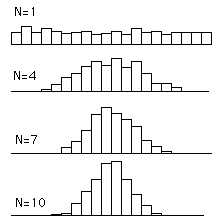
上图中,随着统计量个数的增加,它们和的平均值越来越符合正态分布。
根据中心极限定理,如果一个事物受到多种因素的影响,不管每个因素本身是什么分布,它们加总后,结果的平均值就是正态分布。
举例来说,人的身高既有先天因素(基因),也有后天因素(营养)。每一种因素对身高的影响都是一个统计量,不管这些统计量本身是什么分布,它们和的平均值符合正态分布。(注意:男性身高和女性身高都是正态分布,但男女混合人群的身高不是正态分布。)
许多事物都受到多种因素的影响,这导致了正态分布的常见。
读到这里,读者可能马上就会提出一个问题:正态分布是对称的(高个子与矮个子的比例相同),但是很多真实世界的分布是不对称的。
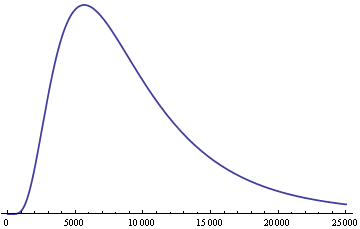
比如,财富的分布就是不对称的,富人的有钱程度(可能比平均值高出上万倍),远远超出穷人的贫穷程度(平均值的十分之一就是赤贫了),即财富分布曲线有右侧的长尾。相比来说,身高的差异就小得多,最高和最矮的人与平均身高的差距,都在30%多。
这是为什么呢,财富明明也受到多种因素的影响,怎么就不是正态分布呢?
原来,正态分布只适合各种因素累加的情况,如果这些因素不是彼此独立的,会互相加强影响,那么就不是正态分布了。一个人是否能够挣大钱,由多种因素决定:
- 家庭
- 教育
- 运气
- 工作
- ...
这些因素都不是独立的,会彼此加强。如果出生在上层家庭,那么你就有更大的机会接受良好的教育、找到高薪的工作、遇见好机会,反之亦然。也就是说,这不是 1 + 1 = 2 的效果,而是 1 + 1 > 2。
统计学家发现,如果各种因素对结果的影响不是相加,而是相乘,那么最终结果不是正态分布,而是对数正态分布(log normal distribution),即x的对数值log(x)满足正态分布。
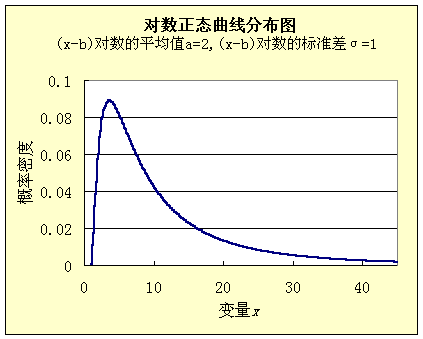
这就是说,财富的对数值满足正态分布。如果平均财富是10,000元,那么1000元~10,000元之间的穷人(比平均值低一个数量级,宽度为9000)与10,000元~100,000元之间的富人(比平均值高一个数量级,宽度为90,000)人数一样多。因此,财富曲线左侧的范围比较窄,右侧出现长尾。
参考链接
- Why isn't everything normally distributed?, by John D. Cook
- Achievement is not normal, by John D. Cook
(完)


szpzs 说:
"原来,正态分布只适合各种因素累加的情况,如果这些因素不是彼此独立的,会互相加强影响,那么就不是正态分布了。" -- 难怪富人越富,穷人越穷。
2017年8月 2日 08:16 | # | 引用
PeterParker 说:
本文中所说的那种对称的正态分布应该是标准正态分布
2017年8月 2日 08:35 | # | 引用
业余草 说:
正态分布好像是高中的内容吧,都忘记完了!
2017年8月 2日 09:32 | # | 引用
xuefliang 说:
看统计书没明白,咋看你博客一下就懂了?
2017年8月 2日 11:00 | # | 引用
1@2 说:
感谢阮老师,简单易懂!不过要是能再深入讲一下中心极限定理就好了。
———————————————————
有个小miss:
与10,000元~100,000元之间的富人(比平均值高一个数量级,宽度为90,为000)
这里应该是“宽度为90000”?
2017年8月 2日 12:58 | # | 引用
阮一峰 说:
谢谢指出,已经更正。
2017年8月 2日 13:26 | # | 引用
catbaron 说:
不……正太分布就是以μ为对称轴对称的,标准是指的μ为0, σ为1
2017年8月 2日 14:07 | # | 引用
catbaron 说:
这种说法只是把「正太分布」的解释转化为「中心极限定理」吧,实际上「为什么会有中心极限定理」还是没有解释。
我还是觉得你之前的想法是对的,至少是一种中心极限定理的解释。
2017年8月 2日 14:10 | # | 引用
sandy 说:
对的,所以说,判断社会或者某平台是否真的公平竞争的标准,看最后的结果是否符合正态分布。
2017年8月 2日 16:00 | # | 引用
sandy 说:
嘿嘿,还要加一句,为什么各个因素相互影响最后结果不是加法而是乘法呢?
因为,正反馈,各个因素构成循环,在多次循环之后表现出的结果是倍数,其实是累加过程,也就是积分嘛。
2017年8月 2日 16:15 | # | 引用
jasmine 说:
均值为0,标准差为1的才是标准正太分布。正太分布都是对称的,不对称的是偏态分布
2017年8月 2日 16:48 | # | 引用
yisam 说:
讲的不错,点个赞
2017年8月 2日 19:19 | # | 引用
archdevil 说:
正态分布里有自然对数的底,以及圆周率。这些数学常数很有可能是宇宙的框架的基础之一。
2017年8月 2日 20:08 | # | 引用
lion 说:
对数正太分布是否可以再通俗点呢,看图我没看大明白,可能对数我忘光了哈哈,不过还是感谢阮大其他讲的非常通俗易懂
2017年8月 3日 10:45 | # | 引用
bugbot 说:
第二个参考链接与第一个雷同了。
2017年8月 3日 15:11 | # | 引用
wangchao 说:
这个只是结果,并不是原因
2017年8月 4日 08:37 | # | 引用
simoncos 说:
正反馈打破正态分布
2017年8月 4日 17:45 | # | 引用
723649234 说:
正太分布以前看不太懂,今天在你这看懂了,很直观。
2017年8月 9日 12:04 | # | 引用
zhangxiaoping 说:
男女身高、寿命、血压、考试成绩、测量误差等等,都属于正态分布。
-------------------------------------------------------------
这句话显然是错误,统计学家全是骗子、弱智。
比如男女身高。某时刻1000个人,假如这1000个人符合正太分布;考察下一时刻,多了一个人,1001个人,这1001个人的身高也符合正太分布吗?显然不是。
2017年8月17日 20:11 | # | 引用
FURENGETE 说:
基因的遗传结果的统计学概率大概都是这样。
2017年8月19日 01:40 | # | 引用
王晓东 说:
2017年9月 4日 10:49 | # | 引用
harper 说:
江苏的话高中就学了
问个问题,为什么男女一起的身高不符合正态分布呢?性别不也是一个影响因素吗?
2017年9月 7日 17:34 | # | 引用
Windsting 说:
第二个参考链接的网址应该是:
https://www.johndcook.com/blog/2009/09/29/achievement-is-log-normal/
2017年9月10日 13:49 | # | 引用
钱小莲 说:
其实也可以从最大熵的角度去理解。在二阶矩一定的情况下,正态分布的熵是最大的,由于自然界有熵增的规律,正态分布自然也就常见了
2017年9月25日 16:43 | # | 引用
Terry 说:
中心极限定理不是说 不管样本个体本身是什么分布 相同数量的样本均值呈现分布最终接近于正态分布。 主要不是指的是sampling distribution of sampling mean嘛?跟文章里讲的中心极限定理的定义貌似是两件事情?谁来解释一下
2017年11月16日 14:57 | # | 引用
单宝英 说:
您讲的真好
2017年11月17日 16:48 | # | 引用
wynhbh 说:
财富分布不是幂律分布吗(Pareto)
2017年12月18日 10:00 | # | 引用
zzz 说:
如果平均财富是10,000元,那么1000元~10,000元之间的穷人(比平均值低一个数量级,宽度为9000)与10,000元~100,000元之间的富人(比平均值高一个数量级,宽度为90,000)人数一样多。
应该是对数平均财富是10,000元
2017年12月24日 21:23 | # | 引用
天空 说:
数学专业的都知道是中心极限定理。这个都还要拿出来说啊
2017年12月25日 19:18 | # | 引用
a 说:
在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。
性别影响不小,性别并不独立,例如不同性别基因差别就很大
2018年4月11日 17:56 | # | 引用
Seagle 说:
性别与基因,营养并不独立,强相关。同一类目标统计才有统计学意义。男女各自头发的长短可能属于正态分布,但均值一定不为0,在非标准分布的情况下,混合在一起统计会符合吗?
2018年7月23日 18:02 | # | 引用
Blues 说:
请问N=1,到N=10的具体图形是怎么得来的呢?有具体的数据计算过程么?
2018年9月27日 11:26 | # | 引用
Lingtong 说:
这几天看了不少阮先生的文章,大为受用,非常感谢!
2019年1月31日 03:25 | # | 引用
冰山下的鱼 说:
甭管多少人,都符合正太分布。
你没弄明白概率和实际的区别,概率是“期望值”,和发生的实际没有关系。
就好像抛一枚正常的硬币抛了5次都是正面朝上,下一次的抛硬币,正面朝上的概率还是50%。
2019年8月 2日 21:41 | # | 引用
wangxiaofeng 说:
r老师这篇文章很好,深入浅出,受益匪浅
2020年2月15日 15:48 | # | 引用
陈小孩 说:
这也是我很纳闷的,如果算的是条件概率"在前五次抛出都是正面的情况下,第六次抛出是正面的概率是多少",结果还是一样吗?大学概率论有两个问题,
一个是:一家庭恰有两个小孩,一小孩为女,则另一小孩为男的概率为多少?
另一个是:考虑恰有两个小孩的全部家庭,从这些家庭中随机选一孩子,若发现她为女孩,则另一孩子是男孩的概率是多少?
前者是2/3,后者是1/2,十分纳闷@-@
2020年2月27日 14:30 | # | 引用
liuwin7 说:
关键点在于正确理解,独立随机事件。
如果问题2换一种描述,问题就清楚了,“考虑恰有两个小孩的全部家庭,从这些家庭选择一个家庭,是一男一女的概率,是多少”。事件满足独立且随机。
再看问题1,为何是2/3,两个孩子的男女排列和组合,一共就4种,分别是男女、女男,女女,男男,已经知道有一个是女孩,“男男”这种可能就被排除了。
所以可能性就3个(男女、女男,女女),而满足条件的可能性是2个(男女,女男),所以,第一题是,2/3,这个题应该在高中的生物里面会学到。
2020年5月15日 11:06 | # | 引用
liuwin7 说:
Sorry,对第2个问题理解有误。
不知道原文是怎么描述,感觉表达有精简,“若发现她为女孩,则另一孩子是男孩的概率是多少?” 应该是 “若发现她为女孩,则该家庭中,另一孩子是男孩的概率是多少?”
基于此,我的理解,选出一个孩子是女孩这个事件,跟后面那个事件(该家庭的另一个孩子是男孩),之间是没有关系的,相对独立的。而且是随机的。
2020年5月15日 11:31 | # | 引用
月光照在酒瓶上 说:
这本质是应该探求中心极限定理(central limit theorem)为什么那么神奇? 我只能定性的理解成,这里面是大数定律这个简单规律的一种累积后的效果
2021年5月28日 09:25 | # | 引用
笙箫默 说:
同问,财富分布不是幂律分布吗?
2021年10月24日 22:50 | # | 引用
Solas 说:
这么武断的评判统计学家,而事实上却是你没有明白数据的概率分布和实际采样之间的差异,希望五年后的你已经认识到了无知,也收起了傲慢吧
2022年3月29日 16:13 | # | 引用
hongqi 说:
效应是独立的,但乘法性的,是对数正态分布。
如果不是独立就会是幂律分布。
这里讲错了
‘原来,正态分布只适合各种因素累加的情况,如果这些因素不是彼此独立的,会互相加强影响,那么就不是正态分布了。一个人是否能够挣大钱,由多种因素决定:
家庭
教育
运气
工作
...
这些因素都不是独立的,会彼此加强。’
2023年6月 4日 23:08 | # | 引用