(这个系列实在拖得太久,今天是最后一篇。)
上一篇介绍了"威尔逊区间",它解决了投票人数过少、导致结果不可信的问题。
举例来说,如果只有2个人投票,"威尔逊区间"的下限值会将赞成票的比例大幅拉低。这样做固然保证了排名的可信性,但也带来了另一个问题:排行榜前列总是那些票数最多的项目,新项目或者冷门的项目,很难有出头机会,排名可能会长期靠后。
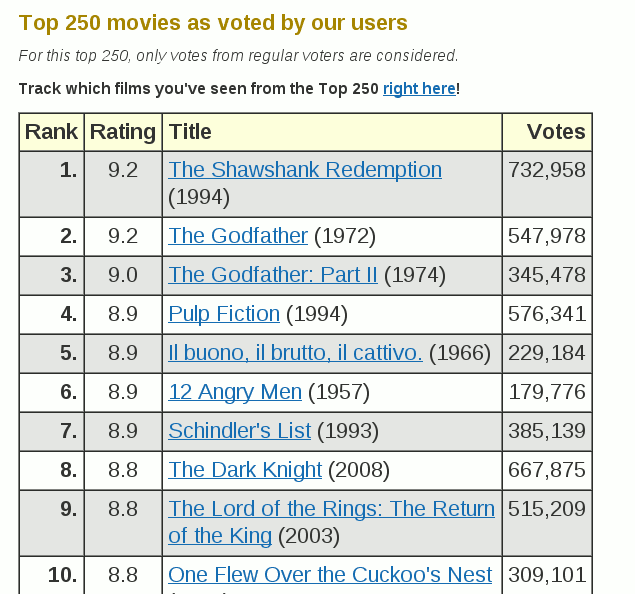
以IMDB为例,它是世界最大的电影数据库,观众可以对每部电影投票,最低为1分,最高为10分。
系统根据投票结果,计算出每部电影的平均得分。然后,再根据平均得分,排出最受欢迎的前250名的电影。
这里就有一个问题:热门电影与冷门电影的平均得分,是否真的可比?举例来说,一部好莱坞大片有10000个观众投票,一部小成本的文艺片只有100个观众投票。这两者的投票结果,怎么比较?如果使用"威尔逊区间",后者的得分将被大幅拉低,这样处理是否公平,能不能反映它们真正的质量?
一个合理的思路是,如果要比较两部电影的好坏,至少应该请同样多的观众观看和评分。既然文艺片的观众人数偏少,那么应该设法为它增加一些观众。
在排名页面的底部,IMDB给出了它的计算方法。
- WR, 加权得分(weighted rating)。
- R,该电影的用户投票的平均得分(Rating)。
- v,该电影的投票人数(votes)。
- m,排名前250名的电影的最低投票数(现在为3000)。
- C, 所有电影的平均得分(现在为6.9)。
仔细研究这个公式,你会发现,IMDB为每部电影增加了3000张选票,并且这些选票的评分都为6.9。这样做的原因是,假设所有电影都至少有3000张选票,那么就都具备了进入前250名的评选条件;然后假设这3000张选票的评分是所有电影的平均得分(即假设这部电影具有平均水准);最后,用现有的观众投票进行修正,长期来看,v/(v+m)这部分的权重将越来越大,得分将慢慢接近真实情况。
这样做拉近了不同电影之间投票人数的差异,使得投票人数较少的电影也有可能排名前列。
把这个公式写成更一般的形式:
- C,投票人数扩展的规模,是一个自行设定的常数,与整个网站的总体用户人数有关,可以等于每个项目的平均投票数。
- n,该项目的现有投票人数。
- x,该项目的每张选票的值。
- m,总体平均分,即整个网站所有选票的算术平均值。
这种算法被称为"贝叶斯平均"(Bayesian average)。因为某种程度上,它借鉴了"贝叶斯推断"(Bayesian inference)的思想:既然不知道投票结果,那就先估计一个值,然后不断用新的信息修正,使得它越来越接近正确的值。
在这个公式中,m(总体平均分)是"先验概率",每一次新的投票都是一个调整因子,使总体平均分不断向该项目的真实投票结果靠近。投票人数越多,该项目的"贝叶斯平均"就越接近算术平均,对排名的影响就越小。
因此,这种方法可以给一些投票人数较少的项目,以相对公平的排名。
=================================================
"贝叶斯平均"也有缺点,主要问题是它假设用户的投票是正态分布。比如,电影A有10个观众评分,5个为五星,5个为一星;电影B也有10个观众评分,都给了三星。这两部电影的平均得分(无论是算术平均,还是贝叶斯平均)都是三星,但是电影A可能比电影B更值得看。
解决这个问题的思路是,假定每个用户的投票都是独立事件,每次投票只有n个选项可以选择,那么这就服从"多项分布"(Multinomial distribution),就可以结合贝叶斯定理,估计该分布的期望值。由于这涉及复杂的统计学知识,这里就不深入了,感兴趣的朋友可以继续阅读William Morgan的How to rank products based on user input。
(完)



ivan 说:
这个系列实在是太好了,看完觉得收获很大!
2012年3月28日 21:15 | # | 引用
glowdan 说:
这个系列不错。reddit以前的和IMDB的以前看过,reddit现在的刚认识。看来还得好好搞下数理统计啊
2012年3月28日 21:47 | # | 引用
abian 说:
这个系列时间差不多一个月吧,不错,下学期的好好复习一下概率论咯。
2012年3月28日 22:42 | # | 引用
码农 说:
博主太强了,膜拜一下
2012年3月29日 00:27 | # | 引用
9527 说:
总算完了!
2012年3月30日 14:36 | # | 引用
莫逢 说:
最近在用贝叶斯统计做垃圾广告的过滤算法,多有互通之处。
感叹一句贝叶斯的智慧和伟大啊。
2012年3月30日 15:28 | # | 引用
如果云知道 说:
老师~我上过您的课~~
来此膜拜下~
2012年3月30日 17:04 | # | 引用
Ralph_adu 说:
不错,这排名还可以应用到其他方面,学习了!
2012年3月31日 08:28 | # | 引用
杨少波 说:
可以收集起来出一本书了,谢谢你的文章!
2012年3月31日 18:04 | # | 引用
老好人 说:
挺好的! IMDB的方法若变换为WR=( v / (v+m)) (R-C) +C 也可能促进理解
2012年4月 1日 11:01 | # | 引用
想~~~ 说:
今天怎么上不去你的博客了?我翻墙上来了...被和谐了???
2012年4月 5日 11:57 | # | 引用
dk01 说:
佩服博主能高质量的完成这么有价值的文章
2012年4月 5日 14:29 | # | 引用
ShiningRay 说:
正好自己的网站也要用到!!!
2012年4月 6日 23:49 | # | 引用
Dell Zhang 说:
Dell Zhang, Robert Mao, Haitao Li, and Joanne Mao. How to Count
Thumb-Ups and Thumb-Downs: User-Rating based Ranking of Items from an
Axiomatic Perspective. In Proceedings of the 3rd International
Conference on the Theory of Information Retrieval (ICTIR), Bertinoro,
Italy, Sep 2011.
http://goo.gl/b3QyX
http://goo.gl/2Ama4
2012年4月 8日 20:09 | # | 引用
摸象 说:
这个系列太棒了!感谢分享!
2012年4月28日 12:59 | # | 引用
随机导弹 说:
这样补一些平均选票,有什么意义?不太懂
这样小众电影的分数会比初始评分更趋向于平均值,即高分变平庸,低分变中等。
求解
2012年5月18日 21:45 | # | 引用
feng 说:
都看完了,收获非常大,可悲,这些知识都还给学校了,当时要是能结合这些应用实例来学习多好
2012年7月25日 11:39 | # | 引用
aaaa 说:
楼上人的回答让我明白了学习其他语言的必要性
2013年12月21日 02:48 | # | 引用
膜拜老师您 说:
受益匪浅
2014年2月 8日 09:25 | # | 引用
tanleihaoren 说:
很好奇这些公式是如何被推导出来的?完全自己想象的么
2014年2月25日 17:45 | # | 引用
B 说:
我最近正好在弄网站的内容排名,能找到您的文章真的太棒了!非常感谢!
2014年4月28日 15:11 | # | 引用
vark 说:
个人觉得这3000张选票只是在排序的时候才会被用到,而不会影响原有的电影评分,只是影响排名而已。
2014年10月15日 17:11 | # | 引用
Iceyl 说:
受益匪浅
2015年2月 5日 17:24 | # | 引用
cccc 说:
感觉这个系列文章没有讲到权重排序的本质是什么..........
权重排序的本质我认为应该是:
各个参数对排序权重的影响,这些参数对于权重分数的影响比例,比如0.2a,0.8a或者a^1.2等等
2015年6月 6日 14:08 | # | 引用
胡子拉碴 说:
赞,这个系列经久不衰,依然受用
2018年12月18日 16:57 | # | 引用
LittleBoy 说:
最后那篇文章的链接打不开。我想看看那篇文章,能发那篇文章的链接给我吗?谢谢
2020年5月14日 13:39 | # | 引用
Shard Zhang 说:
贝叶斯平滑,在推荐算法中的物品点击率统计中常用到
2023年11月 5日 17:27 | # | 引用