一年前的这个时候,我正在翻译Paul Graham的《黑客与画家》。
那本书的第八章,写了一个非常具体的技术问题----如何使用贝叶斯推断过滤垃圾邮件(英文版)。
我没完全看懂那一章。当时是硬着头皮,按照字面意思把它译出来的。虽然译文质量还可以,但是心里很不舒服,下决心一定要搞懂它。
一年过去了,我读了一些概率论文献,逐渐发现贝叶斯推断并不难。原理的部分相当容易理解,不需要用到高等数学。
下面就是我的学习笔记。需要声明的是,我并不是这方面的专家,数学其实是我的弱项。欢迎大家提出宝贵意见,让我们共同学习和提高。
=====================================
贝叶斯推断及其互联网应用
作者:阮一峰
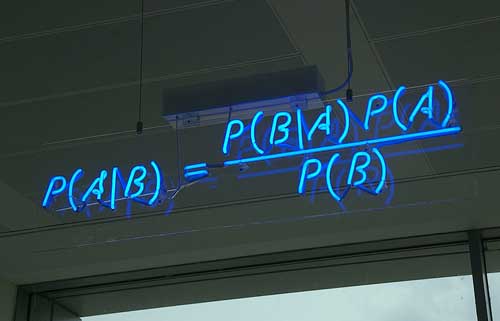
一、什么是贝叶斯推断
贝叶斯推断(Bayesian inference)是一种统计学方法,用来估计统计量的某种性质。
它是贝叶斯定理(Bayes' theorem)的应用。英国数学家托马斯·贝叶斯(Thomas Bayes)在1763年发表的一篇论文中,首先提出了这个定理。

贝叶斯推断与其他统计学推断方法截然不同。它建立在主观判断的基础上,也就是说,你可以不需要客观证据,先估计一个值,然后根据实际结果不断修正。正是因为它的主观性太强,曾经遭到许多统计学家的诟病。
贝叶斯推断需要大量的计算,因此历史上很长一段时间,无法得到广泛应用。只有计算机诞生以后,它才获得真正的重视。人们发现,许多统计量是无法事先进行客观判断的,而互联网时代出现的大型数据集,再加上高速运算能力,为验证这些统计量提供了方便,也为应用贝叶斯推断创造了条件,它的威力正在日益显现。
二、贝叶斯定理
要理解贝叶斯推断,必须先理解贝叶斯定理。后者实际上就是计算"条件概率"的公式。
所谓"条件概率"(Conditional probability),就是指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
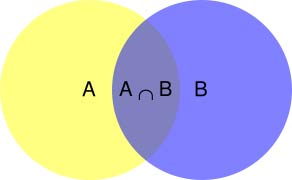
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
因此,
同理可得,
所以,
即
这就是条件概率的计算公式。
三、全概率公式
由于后面要用到,所以除了条件概率以外,这里还要推导全概率公式。
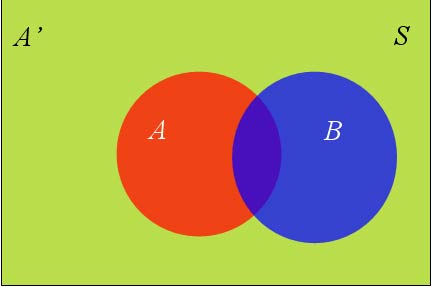
假定样本空间S,是两个事件A与A'的和。

上图中,红色部分是事件A,绿色部分是事件A',它们共同构成了样本空间S。
在这种情况下,事件B可以划分成两个部分。
即
在上一节的推导当中,我们已知
所以,
这就是全概率公式。它的含义是,如果A和A'构成样本空间的一个划分,那么事件B的概率,就等于A和A'的概率分别乘以B对这两个事件的条件概率之和。
将这个公式代入上一节的条件概率公式,就得到了条件概率的另一种写法:
四、贝叶斯推断的含义
对条件概率公式进行变形,可以得到如下形式:
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率 x 调整因子
这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
五、【例子】水果糖问题
为了加深对贝叶斯推断的理解,我们看两个例子。
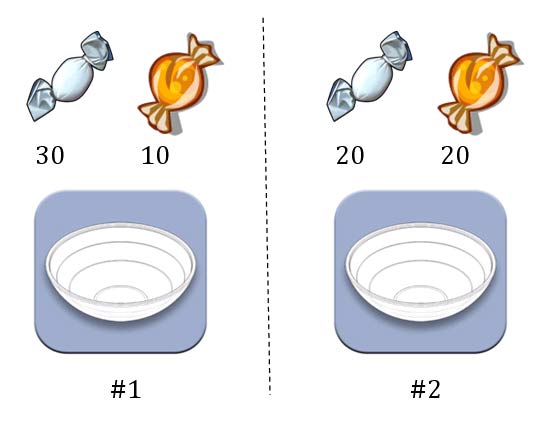
第一个例子。两个一模一样的碗,一号碗有30颗水果糖和10颗巧克力糖,二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗,从中摸出一颗糖,发现是水果糖。请问这颗水果糖来自一号碗的概率有多大?
我们假定,H1表示一号碗,H2表示二号碗。由于这两个碗是一样的,所以P(H1)=P(H2),也就是说,在取出水果糖之前,这两个碗被选中的概率相同。因此,P(H1)=0.5,我们把这个概率就叫做"先验概率",即没有做实验之前,来自一号碗的概率是0.5。
再假定,E表示水果糖,所以问题就变成了在已知E的情况下,来自一号碗的概率有多大,即求P(H1|E)。我们把这个概率叫做"后验概率",即在E事件发生之后,对P(H1)的修正。
根据条件概率公式,得到
已知,P(H1)等于0.5,P(E|H1)为一号碗中取出水果糖的概率,等于0.75,那么求出P(E)就可以得到答案。根据全概率公式,
所以,
将数字代入原方程,得到
这表明,来自一号碗的概率是0.6。也就是说,取出水果糖之后,H1事件的可能性得到了增强。
六、【例子】假阳性问题
第二个例子是一个医学的常见问题,与现实生活关系紧密。

已知某种疾病的发病率是0.001,即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病,它的准确率是0.99,即在患者确实得病的情况下,它有99%的可能呈现阳性。它的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性。现有一个病人的检验结果为阳性,请问他确实得病的可能性有多大?
假定A事件表示得病,那么P(A)为0.001。这就是"先验概率",即没有做试验之前,我们预计的发病率。再假定B事件表示阳性,那么要计算的就是P(A|B)。这就是"后验概率",即做了试验以后,对发病率的估计。
根据条件概率公式,
用全概率公式改写分母,
将数字代入,
我们得到了一个惊人的结果,P(A|B)约等于0.019。也就是说,即使检验呈现阳性,病人得病的概率,也只是从0.1%增加到了2%左右。这就是所谓的"假阳性",即阳性结果完全不足以说明病人得病。
为什么会这样?为什么这种检验的准确率高达99%,但是可信度却不到2%?答案是与它的误报率太高有关。(【习题】如果误报率从5%降为1%,请问病人得病的概率会变成多少?)
有兴趣的朋友,还可以算一下"假阴性"问题,即检验结果为阴性,但是病人确实得病的概率有多大。然后问自己,"假阳性"和"假阴性",哪一个才是医学检验的主要风险?
===================================
关于贝叶斯推断的原理部分,今天就讲到这里。下一次,将介绍如何使用贝叶斯推断过滤垃圾邮件。
(未完待续)


cndj 说:
汗, 没看明白翻译出来的? 那时候看书还觉得讲的挺清晰的
2011年8月25日 12:36 | # | 引用
tristan 说:
我现在开始惊叹,当年高数是怎么过的。
2011年8月25日 12:48 | # | 引用
qq 说:
可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)
这个是为什么呢,我连这个很清楚的东西都不太清楚,楼主再讲下
2011年8月25日 13:11 | # | 引用
ssddi456 说:
无责任揭底大约提高五倍约10%.
验证方法患病检出正确率在0.995,未患病检出误报率在0.005时,阳性患病几率也不过六成七
单指标检测的正确率实在不怎么样啊
2011年8月25日 14:00 | # | 引用
ls zhao 说:
哎呀,看到这些就头疼地很。当时把高数糊弄过去了,不过这里讲地好
2011年8月25日 14:11 | # | 引用
resty 说:
@qq
因为A B同时发生的概率为P(A∩B) = P(B) * P(A | B) , 那么P(A | B) = P(A∩B) / P(B)......
2011年8月25日 14:34 | # | 引用
哺风 说:
@qq
“可以很清楚地看到在事件B发生的情况下,事件A发生的 概率 就是P(A∩B)除以P(B)”
原话应为:
“可以很清楚地看到在事件B发生的情况下,事件A发生的 条件概率 P(A|B)就是P(A∩B)除以P(B)”
阮兄的原话参看上下文也没错,原文的概率指的就是条件概率。
2011年8月25日 15:16 | # | 引用
自由国度 说:
不就是概率末。。。概率上过大学的人都要学的吧。
不过最初发现的人还是最牛的
2011年8月25日 16:04 | # | 引用
lesley 说:
如果假阴性率是0.05,检验结果是阴性,患病几率是不是5.05*10-5
2011年8月25日 16:39 | # | 引用
colordancer 说:
“请问这颗水果糖来自一号碗的概率有多大?”
和
“已知,P(H1)等于0.5,P(E|H1)为一号碗中取出水果糖的概率,等于0.75,”
这颗水果糖来自一号碗 和 一号碗中取出水果糖
这两句话不一样吗
2011年8月25日 17:30 | # | 引用
微波信号 说:
今天各种刺激,先是推上看他们讨论微波天线,来着讨论贝叶斯推断,大学各种挂科伤心事涌上心头。
2011年8月25日 18:00 | # | 引用
jlake 说:
为过滤垃圾邮件,曾经用过 POPFile。
从那时候知道了贝叶斯算法这个名词,具体怎么实现从未关心过。
这篇文章算是给我扫盲了。
2011年8月25日 18:04 | # | 引用
isnowfy 说:
可以查看这篇文章个人觉得讲的挺好的http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/
2011年8月25日 19:18 | # | 引用
daiyechu 说:
我可不可以这么理解呢?权当拿出水果糖已经是一定的事件,也就是1。而一碗水中的水果糖占了总水果糖的60%,就可以得出概率是0.6。
2011年8月26日 10:24 | # | 引用
lee 说:
可悲的大学,等我上完了貌似水平还不如我上高中的时候。。。
2011年8月26日 15:58 | # | 引用
NSS 说:
贝叶斯可以说是现代机器学习技术方面的基础,比如大家熟知的搜索引擎,就非常依赖贝叶斯。
单从公式上看可能比较晦涩,画几个简单的集合图形就会非常好理解。
2011年8月27日 12:53 | # | 引用
Allen 说:
那文氏圖很不錯,重溫了上學期學的條件概率。
2011年8月27日 22:35 | # | 引用
happybird 说:
我是这样理解的:
首先:A是黄色,B是蓝色,中间相交的那部分是B盖在A上的部分。
A发生以后B再发生的部分就是相交的那一部分,这一部分在B中的分量是
p(b)分之p(a^b)
2011年8月29日 22:33 | # | 引用
阿四 说:
关于Bayes theorem,陶哲轩(一个年轻有名的数学家)讲到了一个有趣的例子:
https://plus.google.com/114134834346472219368/posts/Vu7aFD8SPB7
2011年9月 2日 20:22 | # | 引用
麦公 说:
难道习题1%我算错了
2011年9月 5日 15:41 | # | 引用
zhaorui 说:
第一个问题,我算出来的结果是大概9%,看到楼上有10%的,不太确定自己的答案。
我的计算公式为:(0.001*0.99)/((0.99*0.001)+(0.01*0.999))
2011年9月11日 23:59 | # | 引用
zhaorui 说:
假阴性把我给绕进去了
计算公式为:(0.999*0.05)/((0.05*0.999)+(0.95*0.99)) ?
结果:0.6 ?
请指教
2011年9月12日 00:12 | # | 引用
tony 说:
呵呵 讲的真清楚。上学时候就没搞明白 这个定理。看来是当时老师太挫了,呵呵。
2011年9月18日 22:28 | # | 引用
bush 说:
這個思路挺好,直接分析關鍵問題,不受分支細節影響
2011年10月18日 21:33 | # | 引用
Peter 说:
阮哥,你好。在第五章里 作者主要表达的意思是 互联网软件(B/S软件)是微机诞生后的最大机会 也提到了用户需要的上网终端应该越来越小巧便捷 最后发展得像手机一样(iphone)同时包括网络浏览器。这一章看的我很兴奋 呵呵
经过思考 我产生了如下疑问:现在智能手机很普遍了 而且浏览器也是必不可少的客户端 但是现在在智能机上并没有出现互联网软件很火的现象 反而是智能机上的客户端软件开发很吃香 像以前PC机开发桌面软件一样 是不是互联网软件只适用于PC机 而且这个机遇已经过了 因为已经产生了好多互联网巨头 gooele facebook amzon等公司 而不适用于智能机上 还是在智能机上的盛行还没来 要等客户端开发热潮退了 才开始盛行 演变规律像在PC机上发生的一样
现在的智能机都支持JavaScript(是不是说的太绝对了) JavaScript有这么逊吗
小弟不才 请阮哥点拨
2011年11月13日 17:18 | # | 引用
LL 说:
两个问题讨论一下:
1、为什么这种检验的准确率高达99%,但是可信度却不到2%?应该不是与误报率有关,而是跟发病率太低有关。即便误报率为0.01,计算出的患病概率为0.049773,尽管比0.019高了3个百分点,但仍难以说明患病的概率。
2、“假阴性”的概率非常小,几乎是0.19的1/100。所以可以认为检出阴性则没有患病的可靠性很高。
2012年3月23日 21:36 | # | 引用
Vaporz 说:
看完以后脑子里突然冒出个感想:“数学就是用一堆显而易见的废话最后得出一个很神奇的结论。”
好像更能理解为什么有人痴迷于数学,而更多的人没有丝毫兴趣了
2012年5月 9日 16:02 | # | 引用
Vaporz 说:
画个文氏图,就马上明白了 :)
2012年5月 9日 16:04 | # | 引用
David 说:
不错,很清楚!
不过 likelihood 教科书里通常翻做似然
2012年5月10日 18:38 | # | 引用
mm 说:
淚流滿面啊,大學時看不懂,今天終於懂了。
2012年7月11日 14:59 | # | 引用
CrazyChris 说:
這裡的P(A|B)应该是真阳性吧
2012年8月 6日 16:34 | # | 引用
柳旭峰 说:
没想到 如果检验呈阳性的话,那么患病的几率为9%,这么低的一个数值!
虽然知道贝叶斯公式,但是没怎么用过。
看来医学上检验一个药品的难度有多大!
2012年8月13日 10:30 | # | 引用
mufasa 说:
P(A|B) = A∩B/B
等号右边的分式中,分母和分子同时除以样本空间(记为S),这样就是P(A∩B)/P(B)
可以参见wiki条件概率:http://zh.wikipedia.org/wiki/%E6%9D%A1%E4%BB%B6%E6%A6%82%E7%8E%87
2012年8月27日 20:37 | # | 引用
riddle 说:
第二个问题的解释不对吧。可信度低是由于P(A)太小,即发病率太低导致的。
2012年10月16日 23:35 | # | 引用
Jim 说:
第二个例子有个关键错误,在阳性情况下确实发病的概率应为P(B|A),而不是P(A|B)。P(A|B)的含义是发病的人被检测为阳性的概率。在文中计算过程中直接取P(B|A)为0.99也有误,应为0.95。
2012年10月17日 18:02 | # | 引用
Jim 说:
Sorry, 刚才理解错了。
2012年10月17日 18:28 | # | 引用
HaHax 说:
2013年1月16日 15:41 | # | 引用
xwc 说:
怎么没人给出假阴性的答案呢?我算的是1.05E-05,不知道对不,有点绕进去了。
2013年1月18日 19:10 | # | 引用
Chang 说:
我算的是0.0000105367
2013年2月 7日 22:07 | # | 引用
kevin 说:
算对了,看来我看懂了啊
2013年6月20日 17:07 | # | 引用
ahuang1900 说:
你说的对
2013年7月27日 12:43 | # | 引用
shredderming 说:
以前学的时候没想太多,现在想通了。如果用面积表示,那么P(A)=Sa/S,P(B)=Sb/S,P(AB)=Sab/S.
现在要求B发生的情况下,A发生的概率,其实就是AB同时发生的概率(B已经发生,A再发生不就是AB同时发生吗),只不过此时B发生的概率为1.
就是P(B)=Sb/S=1,此时Sb=S。AB同时发生的概率为P(AB)=Sab/S=Sab/Sb。其实这就是条件概率公式了。因为P(A|B)=P(AB)/P(B)=(Sab/S)/(Sb/S)=Sab/Sb。
2013年9月21日 00:48 | # | 引用
wtl 说:
1.05E-05 +1
可见如果是阳性而被漏过的概率很低
宁可误杀 不可错过
2013年9月22日 11:10 | # | 引用
èr.everfly 说:
阴性计算公式:
仍然用A表示发病,用Y表示为阴性,则
P(A|Y) = P(A)*P(Y|A) / P(Y)
= P(A)*P(Y|A) / ( P(A)*P(Y|A) + P(A')*P(Y|A') )
= 0.001*0.01/(0.01*0.001+0.95*0.999)
= 1.053674161802204286346490211367e-5
其实分母中的一部分和分子是相同的。
所以医学检测中,检测结果若为阴性,结果有误的概率非常小,因此结果为阴性的被检测者可以不去复查了。
阳性的话,根据推算可知,误报率比较高,需要进一步、最好使用其他方式复查。
2013年11月21日 11:17 | # | 引用
Albert Yu 说:
@Peter:
现在的智能机(浏览器)都支持 JavaScript,这句话如何推导出 “JavaScript 有这么逊” 来的?这不是恰恰证明了 JavaScript 很强吗?
对于你的问题,其实背后的原因蛮复杂,但是有一个原因绝对是决定性的:web app(也就是你说的互联网软件)所需要的生存环境(即智能机上的浏览器)还不足以完全替代智能机的原生环境。但是这个差距正在快速缩小,你期待的时机也在逐渐到来。
2014年3月21日 01:00 | # | 引用
刀尖红叶 说:
通俗易懂
2014年4月 7日 17:44 | # | 引用
khejing 说:
计算过程中好多图片放在谷歌的服务器上,都看不到呀,阮哥能否换个地方?
2014年6月11日 16:51 | # | 引用
mozart0 说:
毛。试试假设A碗里有水果糖30个巧克力糖无穷个
2014年6月24日 01:03 | # | 引用
Owen 说:
阮老师,你这个页面有一些图片是googleapis.com中的图片,由于最近google国内封的比较厉害,这个图片都没办打开了。能不能把这换成国内的.
2014年8月23日 21:49 | # | 引用
jazz 说:
> 在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强
P(B|A)/P(B)>1 这个可能答应1吗?P(B|A) 肯定比P(B) 小啊
2014年9月10日 16:44 | # | 引用
jazz 说:
这里的P(B|A) 不能理解为 P(A) * P(B)
2014年9月10日 18:15 | # | 引用
wangxing 说:
我是大陆访问的,发现大多数图片都看不到,是否因为是和谷歌有关呢,我们这里无法访问google
2014年9月28日 15:54 | # | 引用
李霞 说:
图片看不见
2014年10月 4日 00:47 | # | 引用
zussy 说:
2014年12月11日 22:56 | # | 引用
匿名 说:
至少高中的时候对概率好熟悉
2015年4月17日 17:07 | # | 引用
abc 说:
显然不对,如果第一个碗是有无穷个巧克力糖,30个水果糖,如果拿到的是水果糖的话,来自第一个碗的几率接近为0,这个算一下就知道了。 直观的意义也很容易理解,反过来假设如果我们选的碗不幸是第一个,那么基本不大可能拿到水果糖,因为它都被巧克力糖淹没了,可以认为如果我们拿到的是水果糖,那么它基本必定是从第二个碗拿到的,由此得出是第一个碗的几率为0.
2015年4月23日 14:57 | # | 引用
bowman 说:
为什么大部分图片都看不了?????
2015年5月 5日 18:46 | # | 引用
呼呼 说:
我的理解,这颗水果糖来自一号碗的概率=一号碗里水果糖的数量/水果糖总数量,一号碗里取出水果糖的概率=一号碗里水果糖的数量/一号碗里糖的总数量,我的疑问是:一号碗里水果糖的数量已知,30,水果糖的总量也知道,50,30/50=0.6,跟条件概率公式算的也一样,为啥要那么麻烦的用条件概率算
2015年9月15日 21:36 | # | 引用
啦啦啦啦啦 说:
感觉糖果的概率算得不太对。
按照公式:后验概率 = 先验概率 x 调整因子
假设碗#1为H1,水果糖为E,则
计算第一次摸出水果糖时,碗为#1的概率公式可表示为:
P(H1|E) = P(H1) x P(E|H1)/P(E)
P(H1) = 0.5
P(E|H1) = 0.75
无异意
但是,P(E)等于多少?
2015年10月 3日 10:24 | # | 引用
啦啦啦啦啦 说:
P(E)是取出水果糖的概率,由于两个碗中水果糖的比例不同,不能简单地用50/80来计算,
而应该通过每次取出糖果来计算概率,
假如第一次取出的是水果糖,则概率为1/1,即100%
则第一次取出糖后,是碗#1的概率
P(H1|E) = 0.5 x 0.75/1
2015年10月 3日 10:34 | # | 引用
GoodJob 说:
讲的真好!!
2015年10月21日 20:16 | # | 引用
有风无风 说:
误报率是5%时,假阴性约为3%,即是在有病的情况下判断为阴性的概率为3%,用假阴性更合理。
2015年12月27日 00:18 | # | 引用
魏志鹏 说:
http://math.stackexchange.com/questions/469974/why-would-i-use-bayes-theorem-if-i-can-directly-compute-the-posterior-probabili
看到这个,感觉还是有一点区别。
2016年1月 8日 09:59 | # | 引用
rainbow702 说:
(0.01 * 0.001) / (0.01 * 0.001 + 0.95 * 0.999) = 1.053674161802204286346490211367e-5
我跟你算的一样
2016年4月12日 10:07 | # | 引用
小邦 说:
我感觉跟大环境相关。这台机器参数性能是固定的,可变的只是环境(先验)。极端地说,如果在发病率为0的环境下,机器的可信度就是0(无论误报率如何);在发病率100%的环境下,机器的可信度就是100%(无论误报率如何)。如果把这台机器放到一个发病率50%的环境里,机器的可信度就跟准确率一致了。
2016年5月22日 22:14 | # | 引用
Gecko 说:
你把1号盘的水果糖和巧克力糖个数分别改成20个和20个,与2号盘完全一样,你再算一下试试。
2016年11月14日 20:29 | # | 引用
cherishcn 说:
阮先生:
其实您的思想和观点我90%以上是赞同的,科研、学历对市场来说对大部分人来说却是没多大意义。只是我想说一句:您的东西里有些东西消极了,小孩不一定能理解。他们可能会误解里面的思想观点。
您比我稍长几岁,您经历过的,也是我正在经历的。是什么情况,我心里也清楚了。
但对90后来说,稍显灰色了。
2016年11月16日 08:22 | # | 引用
cherishcn 说:
前阵子仔细读了您的大作和译著,有感而发。
发表在这一贴因为我把这一页收藏了。经常来读。
2016年11月16日 08:25 | # | 引用
cymurs 说:
博主的问题是:检测出阴性,而真实情况是发病 的概率,你这0.999(不发病的概率)来这凑什么热闹?!!!
2017年1月 5日 11:59 | # | 引用
木子二月鸟 说:
同样的问题,阮老师能不能把这篇里的图片更新一下啊。。。。
2017年2月20日 10:36 | # | 引用
Alan 说:
这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
这句话是我要找的,谢楼主
2017年3月 3日 16:53 | # | 引用
billy 说:
假阴性的概率极低,因为检测出阳性的概率足够高。
这个说明应该保守治疗啊,看到阳性不要慌,可能是误报,看到阴性就把心放肚子里吧
2017年3月 4日 12:31 | # | 引用
Jarhf 说:
2017年8月 1日 11:41 | # | 引用
JI 说:
谢谢!比之前看另外一本书书的时候,理解起来容易很多。图很有帮助
2017年8月 1日 15:50 | # | 引用
cowboy 说:
现有一种试剂可以检验患者是否得病,它的准确率是0.99,即在患者确实得病的情况下,它有99%的可能呈现阳性。这句话是不是有问题啊?按照后面的解释,前面的意思不应该是检验患者得病的准确率是0.99吧,求解答
2017年12月 6日 18:36 | # | 引用
hero_ 说:
在条件(B) 即在患者确实得病的情况下 它有99% (P(A|B))的可能呈现 阳性(事件A)
2018年1月 4日 12:21 | # | 引用
龙谦谦 说:
我算出来也是这个数
2018年2月27日 10:53 | # | 引用
李爽 说:
阮老师,文章的公司图片不翻墙看不了了,可否替换一下啊。
2018年3月 1日 16:45 | # | 引用
colin 说:
图挂了,看不见图片...
2018年3月22日 14:09 | # | 引用
小冰 说:
通俗易懂,十分感谢
2018年5月 5日 16:47 | # | 引用
容儿 说:
对于P(A|B),它的样本空间就变成P(B)了。
2018年5月 7日 11:55 | # | 引用
sun 说:
是的,但“似然”这个翻译其实真的很差,不知道什么意思。可能是很久很久之前的翻译,现在汉语里哪还有人这么说话
2018年5月29日 12:42 | # | 引用
mengshu 说:
明明是概论论好不好
2018年6月29日 09:33 | # | 引用
杨其文 说:
贝叶斯先生1761年就去世了吧,怎么1763年发表论文呢?
2018年7月19日 12:47 | # | 引用
qixinbo 说:
别人帮他发的。。
见:https://en.wikipedia.org/wiki/Thomas_Bayes
2018年7月30日 16:00 | # | 引用
Selina_Zhan 说:
其实这种问题用概率树来解决会好理解的多
2018年9月 9日 17:23 | # | 引用
Zemo 说:
为什么我懂贝叶斯,还是看不懂垃圾邮件识别的算法?
2018年10月30日 18:23 | # | 引用
前端小菜鸡 说:
假阳性问题 得病概率 P(A)=1/1000 阳性概率 分为两种 试剂正常(1/1000*(99/100))和 错误 (999/1000 *(5/100)),p(B) =(1/1000*(99/100))+ (999/1000 *(5/100)),得病是阳性 p(B|A) = (99/100) *P(A)/P(B)
(99/100/1000)/((99/100/1000)+(999/1000*5/100))
0.019434628975265017
2021年2月18日 16:48 | # | 引用
高甜甜 说:
@colordancer:
不一样,人家说的是来自一号碗的概率,而不是取出水果糖的概率。
2021年4月22日 17:04 | # | 引用
生医讯 说:
阮老师好,公众号生医讯(biomedinfo)想转载下您这篇文章,会标明作者和出处,能否授权下?谢谢!
2021年11月 7日 09:28 | # | 引用