上一次,我介绍了贝叶斯推断的原理,今天讲如何将它用于垃圾邮件过滤。
========================================
贝叶斯推断及其互联网应用
作者:阮一峰

(接上文)
七、什么是贝叶斯过滤器?
垃圾邮件是一种令人头痛的顽症,困扰着所有的互联网用户。
正确识别垃圾邮件的技术难度非常大。传统的垃圾邮件过滤方法,主要有"关键词法"和"校验码法"等。前者的过滤依据是特定的词语;后者则是计算邮件文本的校验码,再与已知的垃圾邮件进行对比。它们的识别效果都不理想,而且很容易规避。
2002年,Paul Graham提出使用"贝叶斯推断"过滤垃圾邮件。他说,这样做的效果,好得不可思议。1000封垃圾邮件可以过滤掉995封,且没有一个误判。
另外,这种过滤器还具有自我学习的功能,会根据新收到的邮件,不断调整。收到的垃圾邮件越多,它的准确率就越高。
八、建立历史资料库
贝叶斯过滤器是一种统计学过滤器,建立在已有的统计结果之上。所以,我们必须预先提供两组已经识别好的邮件,一组是正常邮件,另一组是垃圾邮件。
我们用这两组邮件,对过滤器进行"训练"。这两组邮件的规模越大,训练效果就越好。Paul Graham使用的邮件规模,是正常邮件和垃圾邮件各4000封。
"训练"过程很简单。首先,解析所有邮件,提取每一个词。然后,计算每个词语在正常邮件和垃圾邮件中的出现频率。比如,我们假定"sex"这个词,在4000封垃圾邮件中,有200封包含这个词,那么它的出现频率就是5%;而在4000封正常邮件中,只有2封包含这个词,那么出现频率就是0.05%。(【注释】如果某个词只出现在垃圾邮件中,Paul Graham就假定,它在正常邮件的出现频率是1%,反之亦然。这样做是为了避免概率为0。随着邮件数量的增加,计算结果会自动调整。)
有了这个初步的统计结果,过滤器就可以投入使用了。
九、贝叶斯过滤器的使用过程
现在,我们收到了一封新邮件。在未经统计分析之前,我们假定它是垃圾邮件的概率为50%。(【注释】有研究表明,用户收到的电子邮件中,80%是垃圾邮件。但是,这里仍然假定垃圾邮件的"先验概率"为50%。)
我们用S表示垃圾邮件(spam),H表示正常邮件(healthy)。因此,P(S)和P(H)的先验概率,都是50%。
然后,对这封邮件进行解析,发现其中包含了sex这个词,请问这封邮件属于垃圾邮件的概率有多高?
我们用W表示"sex"这个词,那么问题就变成了如何计算P(S|W)的值,即在某个词语(W)已经存在的条件下,垃圾邮件(S)的概率有多大。
根据条件概率公式,马上可以写出
公式中,P(W|S)和P(W|H)的含义是,这个词语在垃圾邮件和正常邮件中,分别出现的概率。这两个值可以从历史资料库中得到,对sex这个词来说,上文假定它们分别等于5%和0.05%。另外,P(S)和P(H)的值,前面说过都等于50%。所以,马上可以计算P(S|W)的值:
因此,这封新邮件是垃圾邮件的概率等于99%。这说明,sex这个词的推断能力很强,将50%的"先验概率"一下子提高到了99%的"后验概率"。
十、联合概率的计算
做完上面一步,请问我们能否得出结论,这封新邮件就是垃圾邮件?
回答是不能。因为一封邮件包含很多词语,一些词语(比如sex)说这是垃圾邮件,另一些说这不是。你怎么知道以哪个词为准?
Paul Graham的做法是,选出这封信中P(S|W)最高的15个词,计算它们的联合概率。(【注释】如果有的词是第一次出现,无法计算P(S|W),Paul Graham就假定这个值等于0.4。因为垃圾邮件用的往往都是某些固定的词语,所以如果你从来没见过某个词,它多半是一个正常的词。)
所谓联合概率,就是指在多个事件发生的情况下,另一个事件发生概率有多大。比如,已知W1和W2是两个不同的词语,它们都出现在某封电子邮件之中,那么这封邮件是垃圾邮件的概率,就是联合概率。
在已知W1和W2的情况下,无非就是两种结果:垃圾邮件(事件E1)或正常邮件(事件E2)。
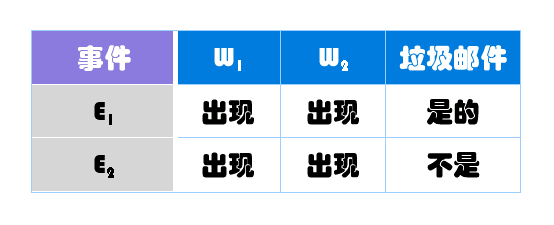
其中,W1、W2和垃圾邮件的概率分别如下:

如果假定所有事件都是独立事件(【注释】严格地说,这个假定不成立,但是这里可以忽略),那么就可以计算P(E1)和P(E2):
又由于在W1和W2已经发生的情况下,垃圾邮件的概率等于下面的式子:
即
将P(S)等于0.5代入,得到
将P(S|W1)记为P1,P(S|W2)记为P2,公式就变成
这就是联合概率的计算公式。如果你不是很理解,点击这里查看更多的解释。
十一、最终的计算公式
将上面的公式扩展到15个词的情况,就得到了最终的概率计算公式:
一封邮件是不是垃圾邮件,就用这个式子进行计算。这时我们还需要一个用于比较的门槛值。Paul Graham的门槛值是0.9,概率大于0.9,表示15个词联合认定,这封邮件有90%以上的可能属于垃圾邮件;概率小于0.9,就表示是正常邮件。
有了这个公式以后,一封正常的信件即使出现sex这个词,也不会被认定为垃圾邮件了。
(完)


49Degree 说:
难怪现在收的开发票垃圾邮件,都是以附件图片显示内容了
2011年8月27日 18:09 | # | 引用
屎蛋 说:
Mark 先!
估计发展一下可以变成炒股公式
2011年8月27日 20:16 | # | 引用
3tgame 说:
将P(S|W1)记为P1,P(S|W1)记为P2
第二个是否应为W2?
2011年8月27日 20:58 | # | 引用
小年 说:
理论性太强啊~~~
2011年8月27日 21:23 | # | 引用
zc 说:
不怕漏,漏一点没关系,怕被误杀
而且中文的是不是还要加语义分析?
2011年8月27日 22:26 | # | 引用
水人 说:
能不能说明文章中一些数据,比如:“如果某个词只出现在垃圾邮件中,Paul Graham就假定,它在正常邮件的出现频率是1%,反之亦然。随着邮件数量的增加,计算结果会自动调整。”中的1%,请问是不是经验值
2011年8月27日 22:48 | # | 引用
Allen 说:
P(E1)+P(E2)不等於1嗎?
2011年8月27日 23:01 | # | 引用
Bill 说:
整个过程讲的很清晰,谢谢阮大哥分享,不过,推导中有两个地方我不太明白:
1. P(E1)=P(S|W1)*P(S|W2)*P(S) (why?)
2. P=P(E1)/(P(E1)+P(E2)) 像楼上Allen说的,直觉是P(E1)+P(E2)=1
能否解释一下E1和E2在样本空间中的精确含义呢?
我的理解是E1=S && W1 && W2,也就是说有E1封邮件,满足以上三个条件,总邮件S+H封,P(E1)=E1/(S+H)
能否解释一下1和2的理由?
谢谢!!
2011年8月28日 00:36 | # | 引用
Paul Graham中文站 说:
本人也是 Paul Graham 的粉丝,也看过你翻译的黑客与画家,
但还是凭直觉认为 PG 不可能是Bayes filtering的发明者,你看看这个就知道了:http://en.wikipedia.org/wiki/Bayesian_spam_filtering#History
96年就有人发布了。
2011年8月28日 08:14 | # | 引用
hyh 说:
看这里, 96年就有人发明了Bayes Filtering, PG怎么可能是发明者。
2011年8月28日 08:15 | # | 引用
new4everlau 说:
挺好的文章,我是来学习的!
在第十一节上面倒数第二行有点表述错误,不过不影响阅读!
“将P(S|W1)记为P1,P(S|W1)记为P2,公式就变成”
“将P(S|W1)记为P1,P(S|W2)记为P2,公式就变成”
2011年8月28日 08:22 | # | 引用
阮一峰 说:
@3tgame:谢谢指出,已经更正了。
@水人:对,是经验值。好在可以根据新收的邮件不断调整。
@Allen:E1和E2是指后面三个事件同时发生,所以它们的和不等于1。
@hyh:Paul Graham发明的是现在这一套计算方法,大大提高了过滤效果,而不是发明用贝叶斯推断过滤邮件的概念。
2011年8月28日 08:24 | # | 引用
阮一峰 说:
E1代表三个独立事件同时发生,因此E1的概率是后面三个概率的乘积。
如果P(E1)=P(S|W1W2),那么P(E1)+P(E2)确实等于1。
但是,我们规定E1是三个事件同时发生,因此P(E1)等于P(W1)P(W2)P(S),所以它与P(E2)的和不会等于1。
2011年8月28日 09:48 | # | 引用
hyh 说:
这类文章真有必要让国内媒体看看。南方周末、南都周刊上面全是垃圾评论,什么炒股赚钱之类。国人人海战术的水平还蛮高的⋯⋯
2011年8月28日 09:57 | # | 引用
天天向上 说:
如果概率论老师能像这样讲些具体应用,我上课也不至于睡觉了
2011年8月28日 14:36 | # | 引用
fengyh 说:
P1应该是P(W1|S)吧?
2011年8月28日 15:15 | # | 引用
mw3000 说:
http://science.solidot.org/article.pl?sid=11/08/06/147202
贝叶斯定理以18世纪的长老教会牧师Thomas Bayes的名字命名,目的是为了解决一些本质问题:当更多信息涌入时我们如何改变信仰?是顽固的直到旧有假说完全站不住脚?还是在怀疑第一次出现后立即抛弃旧观念?贝叶斯的推导已经变成了无价的科学工具,它帮助我们一步步认清现实。也许人人都应该像贝叶斯那样思考。
https://www.nytimes.com/2011/08/07/books/review/the-theory-that-would-not-die-by-sharon-bertsch-mcgrayne-book-review.html
贝叶斯理论的核心依赖于巧妙的转变思路:如果你想评估根据证据提出的假说的有力程度,你必须先评估证据的有力程度。面对着不确定性,贝叶斯提出了三个问题:对最初树立的信念的真实性我有多大的信心?如果对最初的信念坚信不疑,对新证据的准确性我有多大的信心?如果对最初的信念摇摆不定,对新证据的准确性我有多大的信心?大卫·休谟就是一位贝叶斯主义者,他就是通过证据的可能性质疑神迹的准确性。
这一段话我没有看得太懂, 博主能不能帮解释一下.
2011年8月28日 16:34 | # | 引用
cumirror 说:
粗略看了一遍,很精彩的文章。
2011年8月28日 17:13 | # | 引用
呆子 说:
第十步的推导建立在三个量的独立性上,即P(S|W1)、P(S|W2)、P(S),或者说是这三者的相关性很小,可以忽略。但就在这样的基础上,我们得到了
P(S)=P(S|W1)XP(S|W2)/(P(S|W1)XP(S|W2)+(1-P(S|W1))X(1-P(S|W2)))
然而这个关系式很清楚的给出了P(S|W1)、P(S|W2)、P(S)三者的关系。这是不是让我们很遗憾,尽管整个过程是没有问题的,但我们觉得很别扭。由无关的假设,却得到了真真切切的关系。
而笔者似乎忘记了最简单的计算P(S)的方法:
P(S)=P(S|W1)XP(W1)+P(S|W2)XP(W2)+P(S|W3)XP(W3)+……
这里P(W1)P(W2)P(W3)……是W1W2W3出现的频率。
而且这样做是没有理论上的缺陷的。是否可以考虑一下?
2011年8月28日 18:57 | # | 引用
清风剑 说:
对,中文要分词再做以上步骤,但分词就表明了你是怎么理解一个句子的,纠结。。
2011年8月28日 20:31 | # | 引用
Bill 说:
@ Mw3000:
贝叶斯理论的核心依赖于巧妙的转变思路:如果你想评估根据证据提出的假说的有力程度,你必须先评估证据的有力程度。面对着不确定性,贝叶斯提出了三个问题:
对最初树立的信念的真实性我有多大的信心? ---> P(A)
如果对最初的信念坚信不疑,对新证据的准确性我有多大的信心?---> P(B|A)
如果对最初的信念摇摆不定,对新证据的准确性我有多大的信心?---> P(B)
Bayesian Inference:
P(A|B)=P(A)*P(B|A)/P(B)
该文揭示了公式中每一项的现实含义。谢谢分享,我一直在想公式里的每一项有什么直接朴素的内涵,这三个问题回答了我的疑问。
2011年8月28日 23:54 | # | 引用
Chuan 说:
请问有什么即有趣,又实用的概率论方面的书吗?
2011年8月29日 14:31 | # | 引用
Michael.Z 说:
越来越多的邮件采取图片和附件的方式发送垃圾邮件。这方面的鉴别方法又是如何的?
2011年8月29日 16:43 | # | 引用
宁静致远 说:
在华尔街的高频交易系统,70%的股票交易由计算机算法完成,而算法并不总是很可靠。2010年5月算法曾引起股市在短时间内崩盘,它在20分钟内抛出了价值26亿美元的股票,导致其它高频交易算法跟随,引发金融市场混乱。
这种算法的推广的结果是,下个5000天会产生60亿个相当于人脑一样复杂的机器在互联网上.
2011年8月29日 17:04 | # | 引用
mw3000 说:
@Bill:
谢谢你的解释.
2011年8月29日 19:54 | # | 引用
I believe I can fly 说:
不是很明白:
P(S)=p(E1)/(P(E1)+P(E2))
求解释
2011年9月 1日 21:10 | # | 引用
Jin 说:
感觉推导跳过了几步:
P(S|W1 W2) = P(W1 W2|S)P(S) / (P(W1 W2|S)P(S) + P(W1 W2|~S)P(~S))
W1,W2独立:P(W1 W2) = P(W1)P(W2), P(W1 W2|S) = P(W1|S)P(W2|S) (?)
上式 = P(W1|S)P(W2|S)P(S) / (P(W1|S)P(W2|S)P(S) + P(W1|~S)P(W2|~S)P(~S))
应用Bayesian 原理,将 P(Wi|S) 用 P(S|Wi) 表示:
上式 = (P(S|W1)P(S|W2)P(S) * P(W1)P(W2) / P(S)^2) / ((P(S|W1)P(S|W2)P(S) * P(W1)P(W2) / P(S)^2) + (P(~S|W1)P(~S|W2)P(~S) * P(W1)P(W2) / P(~S)^2))
在 P(S) = P(~S) = 50% 的条件下:
上式 = P(S|W1)P(S|W2) / (P(S|W1)P(S|W2) + P(~S|W1)P(~S|W2))
= P1P2 / (P1P2 + (1-P1)(1-P2));
2011年9月 7日 15:26 | # | 引用
fly 说:
根据 Jin 的方法,得到的结果是
p(S|W1W2) = P(~S)P1P2/(P(~S)P1P2 + P(S)(1-P1)(1-P2))
我觉得Jin是正确的。
2011年9月16日 00:13 | # | 引用
ttldreams 说:
现在垃圾留言的干扰符号/文字/异形字越来越多,变种也很多,这种算法奏效吗
2011年9月18日 18:08 | # | 引用
C楠R诺 说:
实在很佩服作者!您的文章给了我学习很大的帮助!非常感谢。
2011年9月24日 19:29 | # | 引用
rrandom 说:
最近在看斯坦福的在线课程.
ml-class.org.对比着这篇文章.收获蛮大..
2011年11月19日 21:12 | # | 引用
fafa 说:
学习了 不过后面的联合概率部分有点懵
2011年11月30日 11:30 | # | 引用
liput 说:
非常感谢你的文章,看了受益匪浅!
2012年2月15日 10:56 | # | 引用
Quady 说:
又由于在W1和W2已经发生的情况下,垃圾邮件的概率等于下面的式子:
P=P(E1)/(P(E1)+P(E2))
我来尝试解释一下,呵呵
在上面已经说明了,E1是在W1和W2同时出现的情况下垃圾邮件的事件,E2是W1和W2同时出现情况下正常邮件的事件,注意这里的前提都是“在W1和W2同时出现的情况下”。
那么,P=P(E1)/P(W1,W2),其意思是W1和W2共同出现的情况下是垃圾邮件的概率,而P(W1,W2)实际就是P(E1)+P(E2)
所以,P=P(E1)/(P(E1)+P(E2))
2012年3月29日 15:42 | # | 引用
futuredo 说:
学习了。贝叶斯公式好像有种能从已然的结果推导出某种原因的意味。
2012年10月22日 12:25 | # | 引用
formath 说:
感觉联合概率那部分虽然最后结果正确,但推倒过程中的独立假设有问题,思路也感觉不太对,还是比较喜欢Jin的思路,简洁清晰。
2013年1月18日 16:34 | # | 引用
alex 说:
作者推导有问题,Jin留言推导的更符合贝叶斯的过程。
btw
P(S|W1 W2) = P(W1|S)P(W2|S)P(S) / (P(W1|S)P(W2|S)P(S) + P(W1|~S)P(W2|~S)P(~S))
已经可以计算出来,为何还要转换成p(S|Wi)呢?
2013年3月19日 15:35 | # | 引用
demo 说:
2013年3月25日 09:55 | # | 引用
bmm 说:
很好的文章,学习了。
2013年3月25日 12:48 | # | 引用
酱油 说:
强大,如果大学老师先把这个例子给我讲了,我大学就不会逃 概率论 这么有用的课了。现在用到了,才知道用处有多大。
2013年3月29日 00:37 | # | 引用
Veronica.C 说:
Jin, 你的解释很赞~~解决了我的疑问!
2013年4月25日 01:15 | # | 引用
Suy 说:
表示正在学概率论……算是一个不错的实际应用举例,涨姿势了~
2013年5月25日 21:17 | # | 引用
liuzhe 说:
记得在《黑客与画家》里看过这个例子
2013年5月27日 20:28 | # | 引用
rude 说:
是不是公式有问题,感觉P(S)=1-(1-P(S|W1)*(1-P(S|W2)*(1-P(S|Wn))
2013年7月 4日 12:06 | # | 引用
gausszh 说:
P(S)=0.5这个假设会不会随着邮件的处理而做修正。但是我们的公式推导中用到了P(S)=0.5。
也就是说P(S)修正后,这个公式推导便不成立了
2013年7月14日 12:04 | # | 引用
Allan 说:
2013年7月14日 14:14 | # | 引用
gausszh 说:
我并不是说错了,文章中有提到“在未经统计分析之前,我们假定它是垃圾邮件的概率为50%。”,那经过统计分析之后呢,随着邮件处理量的增多,这个假设不应修正吗?
2013年7月15日 00:49 | # | 引用
Allan 说:
贝叶斯定理的应用根本上是通过已知概率去获得未知概率的过程,也就是在样本基础上由先验概率去获得后验概率。
放在这个邮件过滤的应用上来说,你的提法“随着邮件处理量的增多”的本意就是样本逐渐扩大,而样本越大则关键字过滤的概率结果越有效。具体到条件概率公示来看,样本扩大仅仅使得P(W|S)、P(W|H)发生了变化,且这个两个概率值是已知的;然而先验的概率P(S)、P(W)依然是已知的,也就是假设的0.5。那么结合起来就能够获得一个更加贴合样本数据(更有效)的后验概率P(S|W)。。。这样也就完成了由已知概率获得未知概率的过程,并且经过大量样本使得这个未知的概率不断得到修正,最后能够得到极为贴合实际的概率结果。从这个角度理解,在贝叶斯定理应用时前提假设的概率一旦给定就大可不必去修改,因为这本就一个合理假定的概率值而已,这个假定值有没有样本都成立。实际对我们所需要获得的后验概率产生影响的是与样本数据有关的概率值,这个值则有关真实性。。。
因为也是自学的这个概念,说的稍微复杂了些,有错误也正常,但希望能启发到你。
2013年7月17日 23:53 | # | 引用
waveacme 说:
我觉得联合概率这部分,虽然阮老师没详细讲清楚,但是他给的链接是讲的很清楚了:
http://www.mathpages.com/home/kmath267.htm
相反,Jin的推导,P(W1 W2|S) = P(W1|S)P(W2|S) 这一步我没理解是怎么得到的,谁能解释一下。
2013年9月24日 14:42 | # | 引用
David_Li 说:
我正在做Bayes Spam Filter作为我的Final Year Project,学习了一下这方面的知识。而且我刚入门的时候也是看的这篇文章。
我纯用公式推导得出的结果也是P(W1,W2|S) = P(W1|S)P(W2|S), 而非作者文中提到的 P(S|W1)P(S|W2)
这个公式是怎么得来的呢?
根据Cox's theorem, 可知P(W1,W2|S) = P(W1|W2,S)*P(W2|S)
http://en.wikipedia.org/wiki/Cox's_theorem
然后W1,W2, ...Wn..都是相互独立的, 所以可以认为P(W1|W2,S) = P(W1|S)
所以, P(W1,W2|S) = P(W1|S)P(W2|S)
Jin的解答中貌似也对这里不太明白。
我是从这篇文章中看到的(第7页)
http://www.mpia-hd.mpg.de/Gaia/publications/class_hrd_q_priors_TN.pdf
我感觉作者用的公式可能不对, 因为我不认为P(S|W1) P(S|W2) P(S)三者是互斥的,也就是说,
P(S|W1)*P(S|W2)*P(S)这个用法是错误的。 (当然也可能是我理解不到位, 请指正)
但Wikipedia上也是用的这个公式, 所以我猜测这可能是为了提高运算效率而做的近似。
因为P(W|S)和P(S|W)在这个公式中其实差不多。
仅是猜测
而根据我的推导, 正确的公式应该是
P(S)*P(W1|S)*P(W2|S) / ( P(S)*P(W1|S)*P(W2|S)+P(~S)*P(W1|~S)*P(W2|~S) )
P(~S) 意为P(Not SPam)
=====================
从小数学就差, 算到这一步智商就已经不够用了。 请大家指正。
总之一句话, 尽信Wiki不如无Wiki
2013年9月29日 20:24 | # | 引用
zhiguoxu2004 说:
呆逼,错了,P(E1) = P(SW1W2) = P(S)*P(W1W2|S) = P(S)*P(W1|S) * P(W2|S)
2013年11月14日 15:36 | # | 引用
呵呵 说:
你的推导是对的,只要对比一个词和十五个词就该知道,十五个词的公式是一个词的公式的推广,不应该是P(S|Wi)的形式,而应该是P(Wi|S)的形式
我正在做Bayes Spam Filter作为我的Final Year Project,学习了一下这方面的知识。而且我刚入门的时候也是看的这篇文章。
我纯用公式推导得出的结果也是P(W1,W2|S) = P(W1|S)P(W2|S), 而非作者文中提到的 P(S|W1)P(S|W2)
这个公式是怎么得来的呢?
根据Cox's theorem, 可知P(W1,W2|S) = P(W1|W2,S)*P(W2|S)
http://en.wikipedia.org/wiki/Cox's_theorem
然后W1,W2, ...Wn..都是相互独立的, 所以可以认为P(W1|W2,S) = P(W1|S)
所以, P(W1,W2|S) = P(W1|S)P(W2|S)
Jin的解答中貌似也对这里不太明白。
我是从这篇文章中看到的(第7页)
http://www.mpia-hd.mpg.de/Gaia/publications/class_hrd_q_priors_TN.pdf
我感觉作者用的公式可能不对, 因为我不认为P(S|W1) P(S|W2) P(S)三者是互斥的,也就是说,
P(S|W1)*P(S|W2)*P(S)这个用法是错误的。 (当然也可能是我理解不到位, 请指正)
但Wikipedia上也是用的这个公式, 所以我猜测这可能是为了提高运算效率而做的近似。
因为P(W|S)和P(S|W)在这个公式中其实差不多。
仅是猜测
而根据我的推导, 正确的公式应该是
P(S)*P(W1|S)*P(W2|S) / ( P(S)*P(W1|S)*P(W2|S)+P(~S)*P(W1|~S)*P(W2|~S) )
P(~S) 意为P(Not SPam)
=====================
从小数学就差, 算到这一步智商就已经不够用了。 请大家指正。
总之一句话, 尽信Wiki不如无Wiki
2013年11月15日 11:37 | # | 引用
kaiye 说:
这个垃圾邮件过滤器有两个细节没弄明白,望阮老师和大神们指教:
1、15个W是怎么挑出来的?如果这个W在垃圾邮件和非垃圾邮件中的词频都很高,比如是“我”这个词,是否有一套筛选原则?
2、为什么公式推导到最后都没有用到 P(W/H),但在一开始的训练集中又被要求计算了这个值。E2事件被定义为正常邮件,文中说P(E2)=(1-P(S|W1))(1-P(S|W2))(1-P(S)),那P(E2)=P(H|W1)P(H|W2)P(H)是否成立?
另外我感觉 Jin 的推导很清晰,其他楼层的同学越说越糊涂,有点误人子弟- -
2013年11月19日 21:47 | # | 引用
翁仁杰 说:
两年前看到的这篇文章,非常感兴趣。这个是我的实现https://github.com/shohoku11wrj/Spam-Filter
,基于Discovery Challenge 2006的一个垃圾邮件过滤竞赛,非常好用的方法,同时也用Logisitic Regression方法实现了一遍。
感谢阮一峰普及了很多计算机和其他方面的知识,还有关于Paul Graham的消息。
实际上Paul Graham关于Spam的一系列文章还有不少,从中也学到了很多。
2013年12月 7日 01:33 | # | 引用
SimonC 说:
我是从《黑客与画家》精装2013年10月第1版找过来的,那里面的P(E1)公式是错误的,最后一个乘数P(S)应为(1-P(S)),另外我想了半天也没理解为什么P(E1)和P(E2)这样算,等我先看看前面的留言。
2014年3月10日 16:17 | # | 引用
Amble 说:
一样可以过滤,因为图片实质是字符流数据,通过分析图像的二进制编码也可以判断
2014年10月22日 05:04 | # | 引用
Amble 说:
另外其实联合概率和P(S)是不是50%无关,只要确保:1.W1,W2..Wn相互独立;2.如果不是垃圾邮件就必然是正常邮件即可:
∵P1=P(S|W1),P2=P(S|W2), P = P(S|W1W2) = P(S∩W1∩W2)/P(W1W2);
又∵P(S∩W1) = P(S|W1)P(W1), P(S∩W2) = P(S|W2)P(W2),
∴P(S∩W1∩W2) = P(S∩W2)∩P(S∩W1) = P(S|W1)P(W1)P(S|W2)P(W2);
而(S∩W1∩W2)+(~S∩W1∩W2)=W1∩W2,
∴P(S|W1W2)=
P(S|W1)P(W1)P(S|W2)P(W2) / [(P(S|W1)P(W1)P(S|W2)P(W2) + P(~S|W1)P(W1)P(~S|W2)P(W2)]; ①
∵P1 = P(S|W1) = P(S∩W1)/P(W1),
P(~S∩W1)/P(W1) = P((1-S)∩W1)/P(W1) = [P(W1)-P(S∩W1)] / P(W1) = 1-P;②
②代入①得到
P = = P1P2 / (P1P2 + (1-P1)(1-P2));
2014年10月24日 03:40 | # | 引用
bo 说:
你好,我现在有一个机器学习作业,看了你写的文章后决定写个垃圾邮件过滤,但是我找不到关于中文的垃圾邮件数据集 不知道您那有相关的数据集可以让我使用一下吗
2014年12月11日 00:41 | # | 引用
stormluke 说:
在原文中似乎并不是选出 P(S|W) 最高的15个词,而是选出 abs(P(S|W) - P(S)) 最高的15个词。
"When new mail arrives, it is scanned into tokens, and the most interesting fifteen tokens, where interesting is measured by how far their spam probability is from a neutral .5, are used to calculate the probability that the mail is spam."
2015年1月 7日 19:58 | # | 引用
hnust_xiehonghao 说:
联合概率那一块 如果没有看懂 可以看下面这个博客中的推导过程:
http://blog.csdn.net/hexinuaa/article/details/5596862
2015年1月 8日 17:33 | # | 引用
markrui 说:
门槛值的设定有没有什么特殊需求,感觉没有理论支持,只是经验使然
2015年4月17日 23:42 | # | 引用
alfred 说:
联合概率推导有问题,P(S|W)是要求解的值,怎么直接用了呢?
P(W|S)才是右边项,作为最大似然估计。
2015年4月21日 16:43 | # | 引用
FlyingWing 说:
这个看着更易懂些。。。太强大了都
2015年4月28日 15:00 | # | 引用
sword 说:
这说明,sex这个词的推断能力很强,将50%的"先验概率"一下子提高到了99%的"后验概率"。
这主要是因为在正常邮件中,sex出现的频率远远低于垃圾邮件。
2015年11月19日 21:19 | # | 引用
incoshare_luo 说:
有PDF格式的吗?第九部分以后图片都无法显示。谢谢
2016年4月19日 16:13 | # | 引用
lanlankk 说:
P(W)这个先验值从何而来没有说明啊?
2016年4月26日 11:39 | # | 引用
ritali 说:
是不是可以用于其他的过滤,比如广告相似的
2016年8月 3日 13:52 | # | 引用
Tim 说:
∴P(S∩W1∩W2) = P(S∩W2)∩P(S∩W1) = P(S|W1)P(W1)P(S|W2)P(W2);
这一步貌似不对
2016年8月31日 17:27 | # | 引用
church 说:
把复杂的东西说的简单易懂.. 感谢
2016年10月 8日 11:33 | # | 引用
温志明 说:
嘻嘻,讨论概率必须区分全局空间和条件空间啊,
p(E1)指的是全局空间下,p(E1)=p(s,w1,w2)=p(s|w1,w2)*p(s) = p(s|w1)*p(s|w2)*p(s)
这不是指在已知w1,w2下邮件为垃圾的概率。
要我这种数学专业才会推倒的。数学+编程+中医,无敌,大家膜拜我吧。
2017年7月27日 01:04 | # | 引用
阿斯蒂芬 说:
联合概率是小数相乘,那么对于python会有溢出的问题?怎么解决呢?
2018年3月13日 20:08 | # | 引用
浅月 说:
请问使用贝叶斯过滤器可以做垃圾广告过滤吗
2018年4月 8日 11:41 | # | 引用
歐子慶 说:
I count the number of times each token (ignoring case, currently) occurs in each corpus.-原文
所以我理解為是算term frequency,不是document number?
2018年12月 8日 20:40 | # | 引用
eli960 说:
贝叶斯过滤垃圾邮件可以做的很好.
这是一个在线的检测垃圾邮件的网址.
http://p.mailhonor.com:25081/demo.html
欢迎讨论
2019年6月 6日 16:35 | # | 引用