大学时,我一直觉得统计学很难,还差点挂科。
工作以后才发现,难的不是统计学,而是我们的教材写得不好。比起高等数学,统计概念其实容易理解多了。
我举一个例子,什么是泊松分布和指数分布?恐怕大多数人都说不清楚。
我可以在10分钟内,让你毫不费力地理解这两个概念。
一、泊松分布
日常生活中,大量事件是有固定频率的。
- 某医院平均每小时出生3个婴儿
- 某公司平均每10分钟接到1个电话
- 某超市平均每天销售4包xx牌奶粉
- 某网站平均每分钟有2次访问
它们的特点就是,我们可以预估这些事件的总数,但是没法知道具体的发生时间。已知平均每小时出生3个婴儿,请问下一个小时,会出生几个?

有可能一下子出生6个,也有可能一个都不出生。这是我们没法知道的。
泊松分布就是描述某段时间内,事件具体的发生概率。
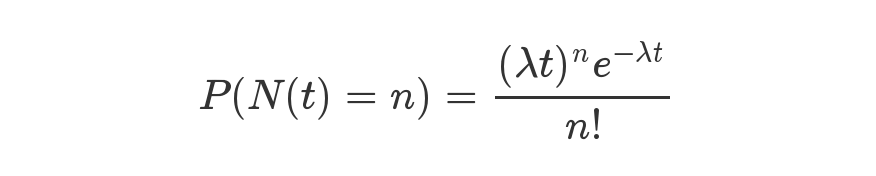
上面就是泊松分布的公式。等号的左边,P 表示概率,N表示某种函数关系,t 表示时间,n 表示数量,1小时内出生3个婴儿的概率,就表示为 P(N(1) = 3) 。等号的右边,λ 表示事件的频率。
接下来两个小时,一个婴儿都不出生的概率是0.25%,基本不可能发生。
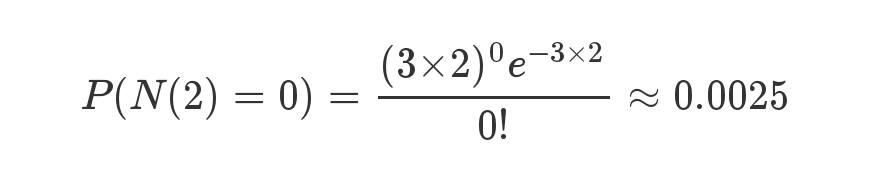
接下来一个小时,至少出生两个婴儿的概率是80%。
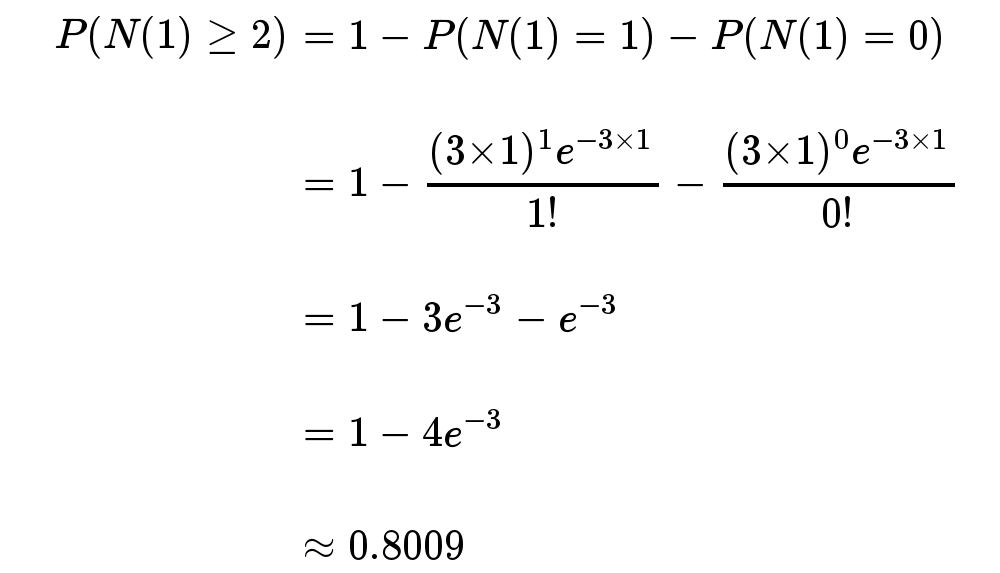
泊松分布的图形大概是下面的样子。
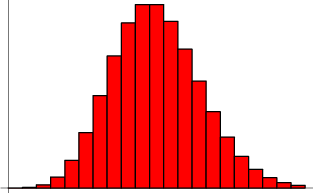
可以看到,在频率附近,事件的发生概率最高,然后向两边对称下降,即变得越大和越小都不太可能。每小时出生3个婴儿,这是最可能的结果,出生得越多或越少,就越不可能。
二、指数分布
指数分布是事件的时间间隔的概率。下面这些都属于指数分布。
- 婴儿出生的时间间隔
- 来电的时间间隔
- 奶粉销售的时间间隔
- 网站访问的时间间隔
指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间 t ,就等同于 t 之内没有任何婴儿出生。
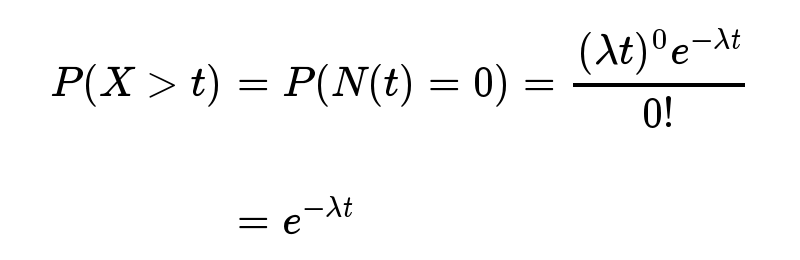
反过来,事件在时间 t 之内发生的概率,就是1减去上面的值。
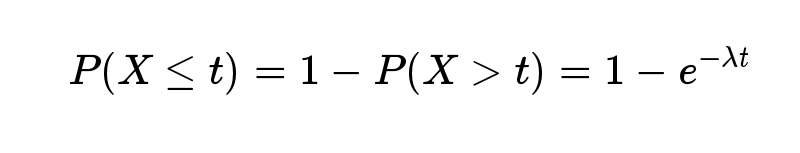
接下来15分钟,会有婴儿出生的概率是52.76%。
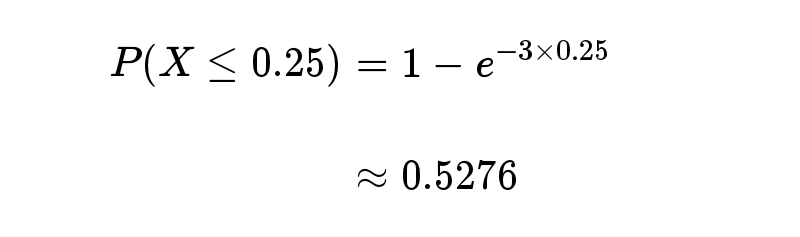
接下来的15分钟到30分钟,会有婴儿出生的概率是24.92%。
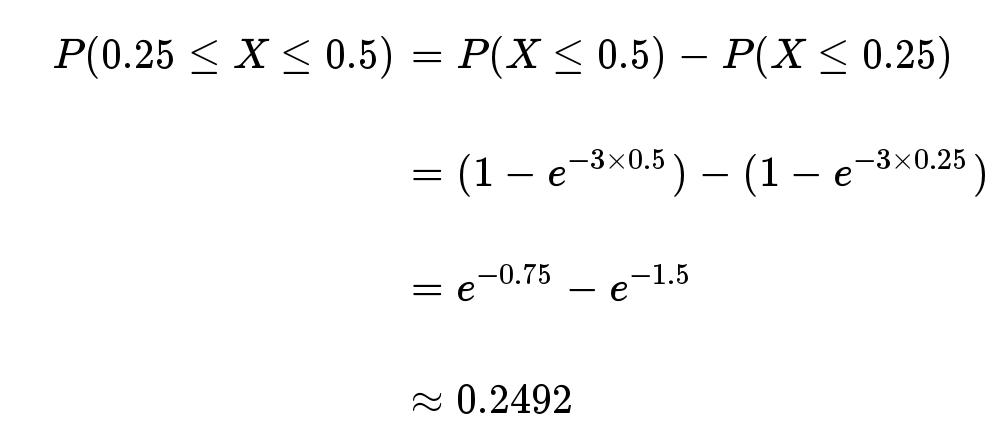
指数分布的图形大概是下面的样子。
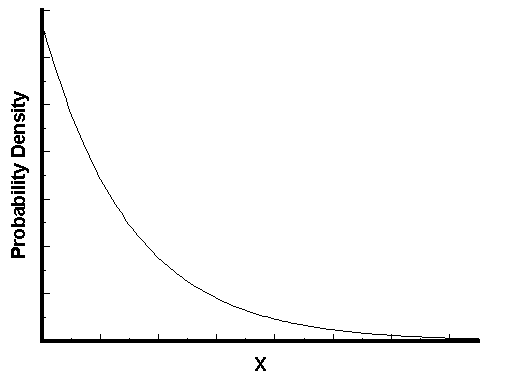
可以看到,随着间隔时间变长,事件的发生概率急剧下降,呈指数式衰减。想一想,如果每小时平均出生3个婴儿,上面已经算过了,下一个婴儿间隔2小时才出生的概率是0.25%,那么间隔3小时、间隔4小时的概率,是不是更接近于0?
三、总结

一句话总结:泊松分布是单位时间内独立事件发生次数的概率分布,指数分布是独立事件的时间间隔的概率分布。
请注意是"独立事件",泊松分布和指数分布的前提是,事件之间不能有关联,否则就不能运用上面的公式。
[说明] 本文受到 nbviewer 文档的启发。
(正文完)
================================================
以下为广告部分。欢迎大家在我的网络日志投放广告,推广自己的产品。
[赞助商广告]
在我之前的博客中,给大家推荐过"帮最优秀的工程师找工作"的 100offer 。时隔半年,我收到了一封朋友来信,讲自己的职业选择,文中也提到了 100offer 。读完后,不禁有些感触,推荐给大家。
08年大学毕业,迄今七年,共有两份工作经历,都在大公司。2011年社招进入华为南研所(南京研究所),从Java+Flex开发到MDE,再后来转SE,在华为来说,这个节奏不算多快但也不算慢,走得挺稳当,与领导、同事相处也很融洽。
只是,渐渐会有一些不安,得空反思,发觉自己在做的这些事,于个人成长而言价值不大。譬如我会用jQuery,它简洁、高效,但我并不知道为何可以这样;再如HashMap、HashTable主要区别在于线程安全与否,但原理是什么我还不清楚??
今年年初,决心离开南研所,并离开南京这座城市......(点击此处阅读原文)
同时决定文尾再帮我的赞助商 100offer 做次推广,1次申请,10个优质offer,1份更好的工作。有需求的程序员们去注册申请拍卖吧。
(完)



伊吕波人 说:
阮兄讲的很清楚。不过学统计学知道这些用处并不是太大。
2015年6月10日 22:46 | # | 引用
Adanov 说:
謝謝你深入淺出的講解。
PS:以前的文章也很有功架,但這篇最讓我讀起來不費勁和容易理解:D,享受學習知識的樂趣,謝謝!
2015年6月10日 22:48 | # | 引用
wahaha 说:
哈哈 大学数理统计100分
2015年6月10日 22:49 | # | 引用
drunkevil 说:
这篇讲的浅显易懂,让我想起了研二时候上的一门随机过程的讨论课。
生活中很多事件都可用泊松分布来讨论。研究中很多的paper都会用泊松分布和泊松过程来建模,物理概念清晰,关键是数学推导完善,看上去相当的完美。
2015年6月10日 22:58 | # | 引用
JokerFun 说:
写的挺好的,不错,继续支持
2015年6月10日 22:58 | # | 引用
n1ceguy 说:
阮老师,
文中第7个公式的左边是不是应为 P(0.25
2015年6月10日 23:51 | # | 引用
阮一峰 说:
@n1ceguy:
谢谢指出,已经改正了。
2015年6月11日 07:36 | # | 引用
humoresque 说:
谢谢博主的分享
2015年6月11日 08:25 | # | 引用
jqk6 说:
这个世界中存在完全独立的事件吗?一个人,一方面相信存在蝴蝶效应,一方面又应用独立事件的概率论知识,大脑为什么不糊涂呢?大脑是如何摆脱这种矛盾的困扰的呢?
2015年6月11日 09:58 | # | 引用
hilojack 说:
我觉得,蝴蝶效应与事件的独立性并不冲突。在蝴蝶效应中,蝴蝶振翅这一事件本向起决定性的作用而已,而其它的事件只是充当配角。正如,木桶原理中最短的板子,多米诺骨中的第一块牌。他们有一个共同的特点:它们是一个极不平衡不稳定的系统,其中最不稳定的因子就充当了蝴蝶的角色。
这个世界中存在完全独立的事件吗?我觉得这取决于视角。脑洞一下:物理上两块物体可能相互独立吗? 从引力场上看好像是不可能的,从平行宇宙上看又好像是
概率统计和蝴蝶效应有什么关系呢?前者描述了一种统计规律;后者描述了一种小变量引发的系统质变,后者只是一种现象。
2015年6月11日 11:20 | # | 引用
lot 说:
顺便搜了一下「泊松分布」, 本来打算看维基的定义的, 结果发现阮老师的另外一篇也在前面的位置.
http://www.ruanyifeng.com/blog/2013/01/poisson_distribution.html
这应该不算是独立事件了吧 (笑~)
2015年6月11日 16:52 | # | 引用
呵呵呵 说:
2015年6月11日 19:44 | # | 引用
Spybdai 说:
从平行宇宙的角度,为何两个物体可以是完全独立的??
2015年6月11日 20:52 | # | 引用
juwan 说:
我竟然看懂了, 大赞,哈哈
2015年6月12日 09:56 | # | 引用
匿名 说:
阮兄,
"接下来的15分钟到30分钟,会有婴儿出生的概率"这个例子有误。
每个连续的15分钟,事件发生的概率都是相同的。
文中那两个概率直接相减没有意义。
2015年6月12日 10:05 | # | 引用
jean 说:
+1
2015年6月12日 15:41 | # | 引用
rubyu2 说:
看到这里我也有点纳闷,应该是描述不准确。意思应该是:"下一个婴儿在30到45分钟出生的概率"
2015年6月13日 07:16 | # | 引用
张张 说:
首先,泊松分布‘一般情况下/常常’用来表示某段时间时间发生概率/次数,而不是您说的‘就是描述某段时间内,事件具体的发生概率’。同样指数分布也是。
其次,很多公式是有因果的,泊松的概率分布公式,之所以是这样,是由二项分布某值趋于无穷最终趋近于这个公式(另外没有仔细推敲第一个公式的由来和可信性)。这个样子去让人理解泊松分布恐怕即使说理解的很多人其实本质上没有理解。
再者,第三个公式的概率间的减法是怎么回事??这是概率间的计算,不是数值间的计算。
整篇文章我认为疑点重重,看了下您参考的原文,都是一坨英文,实在看不下去(英语烂)
如果是让人理解,理应从本质讲起,严谨推敲。
如果是我理解错误,我在这里先道歉,但希望您给予回复;但如果真的是您也没有理解完善,您的文章已经被转到其他平台了,我看的晕晕乎乎也是醉了。
2015年6月15日 10:22 | # | 引用
Trinity 说:
这些东西再好,也不如一个人的直觉。对于一个对事物有灵敏嗅觉的人,统计分析学科真的是影响判断,在指挥战争等等重要事件中绝对是反面教材。
这些学科注定是科学家美丽的玩物----即使你算出了“接下来两个小时,一个婴儿都不出生的概率是0.25%”和“平均每小时出生3个婴儿”这个前提没有本质的区别:你还是无法把握未来,接下来两个小时还真一个婴儿都没出生...
博主,不要耽误生命。
2015年6月16日 00:13 | # | 引用
林晨 说:
"接下来的15分钟到30分钟,会有婴儿出生的概率" 可以改成 “30分钟内,前15分钟没有婴儿出生,后15分钟有婴儿出生的概率。
2015年6月16日 16:23 | # | 引用
爱国者 说:
大学时代,概率论和数理统计是我比较喜欢的学科之一。概率论来源于赌博,里面有很多经典有趣的案例。我也觉得大学教材过于死板,不够活泼
2015年6月17日 07:11 | # | 引用
往事悠扬 说:
你好,可以转载并保留出处么?
2015年6月22日 12:22 | # | 引用
zhangsp 说:
收获很大
2015年6月23日 09:52 | # | 引用
数学渣渣 说:
刚看了一点,学习总是没耐心。
然而我已经觉得泊松分布在暴力破解网站密码方面会很有用。
先mark。考完试再看
2015年6月24日 21:15 | # | 引用
wayne 说:
工作以后才发现,难的不是统计学,而是我们的教材写得不好。-----
博主能能否推荐 一本 简单 易懂的 统计学好教材
谢谢
2015年6月27日 09:05 | # | 引用
Upknd 说:
我曾经就特别想把所有教材全部都改写一遍。。 我总得把全部内容再简单摘录一遍,有时候甚至用自己超简单的话再写一遍,才能快速理解和记忆教材上的内容
2015年6月29日 15:19 | # | 引用
jony 说:
你这个讲的都是随机过程的内容,是泊松过程。泊松分布是与时间t无关的。
2015年7月10日 19:45 | # | 引用
Aubergine 说:
2015年7月29日 16:01 | # | 引用
Aubergine 说:
事件独不独立取决于了解其中一个事件是否会改变另外一个事件发生的概率.如果从平行宇宙的角度来说的话,可能你所看到的两个物体就分属于不同平行宇宙,所以两个物体就可能是完全独立的。比如“单电子双缝干涉”的电子,通过双缝打在挡板上的电子可能是属于不同世界的电子,那么电子之间有可能就是独立的。
2015年7月29日 16:04 | # | 引用
eer 说:
泊松分布的极限分布是正态分布,正态分布是分布之王,楼主似没有讲这个道理。
2015年8月30日 18:18 | # | 引用
Barcode 说:
谢谢分享!
2015年9月16日 13:33 | # | 引用
Joncle 说:
我正好在学概率论,很受启发啊,赞赞赞!
2015年9月26日 14:19 | # | 引用
Al-asad 说:
感谢阮兄!
正在学习泊松过程,做题一直有疑惑想不通。
将泊松、指数分布结合,让我受益匪浅!
2015年9月29日 22:41 | # | 引用
石樱灯笼 说:
泊松分布和正态分布看起来好像啊
2015年10月15日 09:40 | # | 引用
han 说:
专家
文章中的"接下来",怎么理解?如:接下来15分钟,会有婴儿出生的概率是52.76%。接下来两个小时,一个婴儿都不出生的概率是0.25%,基本不可能发生。
2015年10月15日 14:42 | # | 引用
远航 说:
最后那个图应该是指数分布函数的密度函数吧,指数分布的分布函数肯定是增函数。
2015年12月 2日 21:38 | # | 引用
ERIC LIN 说:
看完比较理解泊松过程了,非常感谢,读书看课本完全看不明白。
2015年12月 9日 21:13 | # | 引用
王东安 说:
我提一个问题:
两个区域A和B,和一个节点的集合S,这个集合S中的节点访问A和B社区的时间间隔都服从指数分布,现在区域A通过这个集合S向区域B发送数据。采用的策略是这个集合S中第一个访问区域A的节点将接受数据,然后将数据发送给区域B,求区域A和区域B之间传输数据的时延期望,求大神解决。
2015年12月28日 13:27 | # | 引用
zhexih 说:
求大哥解释一下,
用泊松分布推出指数分布的那一过程,我转不过弯来。P(X>t)=P(N(t)=0)其中P(X>t)是表示什么意思?表示事件在时间t之外的概率吗?
如果是那不是说明时间大于t至少有一个出生的概率,而P(N(t)=0)是表示时间t内一个也没出生的概率。他们能相等吗?
2016年1月 2日 09:53 | # | 引用
hohomi 说:
泊松分布是给定时间内发生的次数的分布
指数分布是等待下一次发生时间的分布
它们可以分别类比到离散的二项分布、几何分布。
二项分布是n次试验内事件发生的次数的分布
几何分布是下一次试验成功需要经历多少次失败,这个等待次数的分布。
2016年2月18日 17:15 | # | 引用
泊松过程 说:
貌似撸主混淆了泊松过程和泊松分布!
这里说的是泊松过程
2016年3月 3日 10:47 | # | 引用
振清 说:
老师讲的简练。其实泊松分布除了表示表示单位时间内独立事件发生次数的概率分布也还表示单位空间内。Java HashMap 源码注释有提到Poisson_distribution。
2016年5月 7日 12:03 | # | 引用
Illuminati 说:
太棒了啊啊啊啊!!!!!!一下子对二项泊松几何指数四种分布深刻理解了!!!!!谢谢谢谢!!!!!
2016年7月11日 16:31 | # | 引用
GoingMyWay 说:
指数分布是独立事件的时间间隔的概率分布,由于几乎每分钟都有婴儿出生,所以2个小时后有婴儿出生的概率比10分钟后由婴儿出生的概率要小。
2016年9月14日 11:37 | # | 引用
lomot 说:
各种博主我就服你,说得了react,还能在这里给我讲泊松分布!
2016年10月16日 23:40 | # | 引用
某读者 说:
泊松分布用二项分布来解释更直观准确。
2016年10月19日 14:36 | # | 引用
企鹅C 说:
统计并不是无用,例如保险精算,在足够多的投保样本下就可以估算出盈利期望和置信区间,还有就是最近火的一塌糊涂的统计机器学习。
2016年11月11日 12:45 | # | 引用
jindongdong 说:
文字表述确实有些失误,在“会有婴儿出生的概率”前面加一个“才”字就ok了。它表示前15分钟没有婴儿出生,只在接下来的15分钟到30分钟这个时间段出生一名婴儿,这个概率显然不同于每15分钟出生一名婴儿的概率。
2017年3月15日 18:33 | # | 引用
Lin 说:
写的非常好,我在美国学校学的泊松分布和指数分布 刚开始学的时候教授给的概念都偏抽象 这篇文章大大的提升了我对这两个分布的理解 非常感谢
2017年3月18日 03:37 | # | 引用
htliu 说:
2017年4月23日 16:54 | # | 引用
吴小包 说:
为什么泊松分布和指数分布是这样的一个式子呢?~有没有具体的理论呢?就像二项分布,是可以通过我们的常识和排列来推导出二项分布的公式~麻烦您可以回复我一下~~~
2017年5月16日 14:30 | # | 引用
Amanda 说:
清晰易懂,一下就明白了,枉费我之前看了好久的wiki,谢谢博主~
2017年5月20日 14:41 | # | 引用
静水 说:
写的真好,感谢!
2017年7月 4日 16:15 | # | 引用
gwallan 说:
博主,有人抄袭你的文章
https://zhuanlan.zhihu.com/p/27888511
2017年8月21日 18:07 | # | 引用
MemberY 说:
写的很好呀,谢谢博主~~~
2018年3月23日 23:28 | # | 引用
挖煤矿工 说:
统计学很有用的,我现在因为投资,在恶补一些统计学知识
2018年7月31日 15:25 | # | 引用
icaoys 说:
应该是泊松过程,和分布的概念不同。
2019年3月 6日 14:31 | # | 引用
小飞龙 说:
可不可以写一篇关于泊松分布、伽马分布,以及负二项分布的文章,非常期待您的解释,尤其是负二项分布,一直很迷糊
2019年3月26日 19:25 | # | 引用
debugable 说:
您好,java的ConcurrentHashMap里面,当hash桶存储元素达到8个时从链表转为红黑树,计算公式是(exp(-0.5) * pow(0.5, k) / factorial(k))。这个0.5是怎么确认的呢?
2019年12月 9日 20:38 | # | 引用
virtualf 说:
我们的大学教材简直太糟糕了,后来干脆引用国外的教材了。
2020年6月22日 08:58 | # | 引用
影法師 说:
其实,写的并不清楚~
2020年6月27日 09:37 | # | 引用
Yiyan Yang 说:
写的真的棒!谢谢分享
2020年10月 2日 13:23 | # | 引用
huang 说:
发现新大陆
2020年12月27日 13:07 | # | 引用
alextee 说:
卷积呢
2021年3月 3日 23:35 | # | 引用
muye 说:
泊松分布中写到,"λ 表示事件的频率。",这个不对吧,和你例子中的 λ 取 3 完全不是一个含义呀
2021年6月21日 13:55 | # | 引用
奋斗者 说:
厉害!真的看了一下子懂了!佩服!
2021年8月 4日 08:48 | # | 引用
艾丝蒂尔 说:
感谢分享!基本没有统计基础(但是作死选了统计课)的人一下子就懂了
2022年1月14日 11:14 | # | 引用